题目内容
9.设实数x,y满足$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{y≥x}\end{array}\right.$,则x+2y的最小值为( )| A. | 1.5 | B. | 2 | C. | 5 | D. | 6 |
分析 作出不等式组对应的平面区域,利用线性规划的知识即可得到结论.
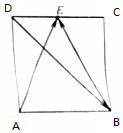
解答  解:作出不等式组$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{y≥x}\end{array}\right.$对应的平面区域如图
解:作出不等式组$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{y≥x}\end{array}\right.$对应的平面区域如图
由z=x+2y得y=-$\frac{1}{2}x$+$\frac{1}{2}z$,
平移直线y=-$\frac{1}{2}x$+$\frac{1}{2}z$,
则当直线y=-$\frac{1}{2}x$+$\frac{1}{2}z$经过点B时,直线在y轴上的截距最小.由:$\left\{\begin{array}{l}{y=x}\\{x+y=1}\end{array}\right.$,可得B($\frac{1}{2}$,$\frac{1}{2}$),
此时z=$\frac{1}{2}+$2×$\frac{1}{2}$=1.5,
故选:A.
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
20.下列函数中,最小值为4的是( )
| A. | y=$\frac{lgx}{2}+\frac{8}{lgx}$ | B. | y=$2\sqrt{{x^2}+2}+\frac{2}{{\sqrt{{x^2}+2}}}$ | ||
| C. | $y=sinx+\frac{4}{sinx}$(0<x<π) | D. | y=ex+4e-x |
4.已知集合M={x||x|≤2},N={x|x2+2x-3≤0},则M∩N=( )
| A. | {x|-2≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1≤x≤2} | D. | {x|-3≤x≤2} |
1.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且$\frac{{S}_{1}}{{S}_{2}}$=$\frac{16}{9}$,则$\frac{{V}_{1}}{{V}_{2}}$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
19.若函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$图象的两条相邻的对称轴之间的距离为$\frac{π}{2}$,且该函数图象关于点(x0,0)成中心对称,${x_0}∈[0,\frac{π}{2}]$,则x0=( )
| A. | $\frac{π}{12}$ | B. | $\frac{5π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
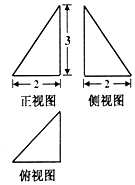 已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.
已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.