题目内容
13.函数f(x)=3sin(3x+$\frac{π}{4}$)的最小正周期为$\frac{2π}{3}$.分析 利用利用函数y=Asin(ωx+φ)的周期为 $\frac{2π}{ω}$,得出结论.
解答 解:函数f(x)=3sin(3x+$\frac{π}{4}$)的最小正周期为$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$.
点评 本题主要考查函数y=Asin(ωx+φ)的周期性,利用了函数y=Asin(ωx+φ)的周期为 $\frac{2π}{ω}$,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知集合M={x||x|≤2},N={x|x2+2x-3≤0},则M∩N=( )
| A. | {x|-2≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1≤x≤2} | D. | {x|-3≤x≤2} |
1.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且$\frac{{S}_{1}}{{S}_{2}}$=$\frac{16}{9}$,则$\frac{{V}_{1}}{{V}_{2}}$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
2.已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{{m}^{2}}$=1(m>0)的焦距为8,则m的值为( )
| A. | 3或$\sqrt{41}$ | B. | 3 | C. | $\sqrt{41}$ | D. | ±3或$±\sqrt{41}$ |
3.若三棱锥的三条侧棱两两垂直,侧棱长分别为1,$\sqrt{3}$,2,且它的四个顶点在同一球面上,则此球的体积为( )
| A. | $\frac{{2\sqrt{2}}}{3}π$ | B. | $3\sqrt{3}π$ | C. | $\frac{{8\sqrt{2}}}{3}π$ | D. | 8π |
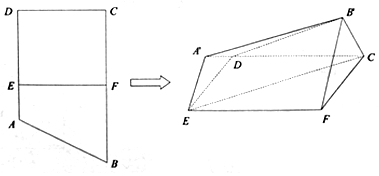
 如图,已知矩形ABCD,AD=2,E为AB边上的点,现将△ADE沿DE翻折至△A′DE,使得点A′在平面EBCD上的投影在CD上,且直线A′D与平面EBCD所成角为45°,则线段AE的长为2$\sqrt{2}$.
如图,已知矩形ABCD,AD=2,E为AB边上的点,现将△ADE沿DE翻折至△A′DE,使得点A′在平面EBCD上的投影在CD上,且直线A′D与平面EBCD所成角为45°,则线段AE的长为2$\sqrt{2}$.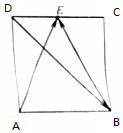
 已知扇环如图所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇环边界上一动点,且满足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则2x+y的取值范围为[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].
已知扇环如图所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇环边界上一动点,且满足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则2x+y的取值范围为[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].