题目内容
8. 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )| A. | 24π | B. | $24π+8\sqrt{2}π$ | C. | $24π+4\sqrt{2}π$ | D. | 32π |
分析 几何体的表面积是圆柱的侧面积与半个求的表面积、圆锥的侧面积的和.
解答 解:圆柱的侧面积为S1=2π×2×4=16π,半球的表面积为${S_2}=2π×{2^2}=8π$,
圆锥的侧面积为${S_3}=\frac{1}{2}×2π×2×2\sqrt{2}=4\sqrt{2}π$,
所以几何体的表面积为$S={S_1}+{S_2}+{S_3}=24π+4\sqrt{2}π$;
故选C.
点评 本题考查了几何体的三视图以及表面积的计算.属于基础题.

练习册系列答案
相关题目
19.已知函数f(x)=log2(a2x-4ax+1),且0<a<1,则使f(x)>0成立的x的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,2loga2) | D. | (2loga2,+∞) |
3.已知命题p:0<a<4,命题q:a(a-4)≤0; 则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
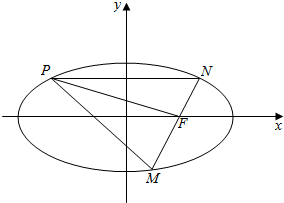 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点P(-2$\sqrt{3}$,1),且离心率e=$\frac{\sqrt{3}}{2}$,过右焦点F的直线l交椭圆于M,N两点.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点P(-2$\sqrt{3}$,1),且离心率e=$\frac{\sqrt{3}}{2}$,过右焦点F的直线l交椭圆于M,N两点.