题目内容
1.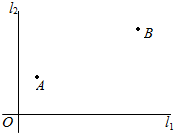 如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.
如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.(1)若出入口P建造在高速公路l1上,求A,B两城居民,“不满意度”的最小值;
(2)试确定出入口P建在高速公路何处,才能使A,B两城居民的,“不满意度”最小?
分析 (1)以l1,l2所在直线为x,y轴建立平面直角坐标系,由此能求出当A1,P,B三点共线时,即点P(40,0)时,M1取最小值,并能求出这个最小值.
(2)若点P在l2上时,设P(0,a),当a=45时,M2取最小值,从而求出出入口P应该建在高速公路l2上,且到点O距离为45km,能够使得A,B城居民的“平均不满意度”最小.
解答  解:(1)以l1,l2所在直线为x,y轴建立如图所示平面直角坐标系,
解:(1)以l1,l2所在直线为x,y轴建立如图所示平面直角坐标系,
则A(20,30),B(80,60)…(2分)
若点P在l1上时,则点A关于则x轴的对称点为A1(20,-30),
故${M_1}=\frac{k}{2}(PA+PB)=\frac{k}{2}(P{A_1}+PB)≥\frac{k}{2}{A_1}B=\frac{k}{2}\sqrt{11700}$
当A1,P,B三点共线时,即点P(40,0)时,M1的最小值为$\frac{k}{2}\sqrt{11700}$.…(8分)
(2)若点P在l2上时,设P(0,a),${M_2}=\frac{k}{2}\sqrt{P{A^2}+P{B^2}}=\frac{k}{2}\sqrt{2{{(a-45)}^2}+7250}$…(12分)
当a=45时,M2的最小值为$\frac{k}{2}\sqrt{7250}$…(14分)
∵$\frac{k}{2}\sqrt{11700}>$$\frac{k}{2}\sqrt{7250}$
∴出入口P应该建在高速公路l2上,且到点O距离为45km,能够使得A,B城居民的“平均不满意度”最小.
答:出入口P建在高速公路l2上,且到点O距离为45km,A,B城居民的“平均不满意度”最小.…(16分)
点评 本题考查A,B两城居民,“不满意度”的最小值的求法,是中档题,解题时要认真审题,注意直线性质的合理运用.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | 3 | B. | $3\sqrt{2}$ | C. | $2+\frac{{\sqrt{2}}}{2}$ | D. | $1+\frac{{3\sqrt{2}}}{2}$ |
| A. | 9π | B. | 8π | C. | $\frac{23}{3}π$ | D. | $\frac{28}{3}π$ |
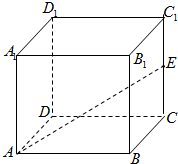 如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)
如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)