题目内容
若直线y=x+b与曲线x=
恰有一个公共点,则b的取值范围是( )
| 1-y2 |
| A、-1<b≤1 | ||
| B、-1≤b≤1 | ||
C、-
| ||
D、-1<b≤1或b=-
|
考点:直线与圆的位置关系
专题:直线与圆
分析:曲线x=
即 x2+y2=1(x≥0)表示一个半径为1的半圆,如图,数形结合求得当直线y=x+b与曲线x=
恰有一个公共点时b的取值范围.
| 1-y2 |
| 1-y2 |
解答:
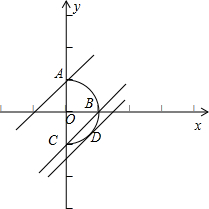 解:曲线x=
解:曲线x=
即 x2+y2=1(x≥0)表示一个半径为1的半圆,如图所示.
当直线y=x+b经过点A(0,1)时,求得b=1,
当直线y=x+b经过点B(1,0)时,求得b=-1,
当直线和半圆相切于点D时,由圆心O到直线y=x+b的距离等于半径,
可得
=1,求得b=-
,或b=
(舍去).
故当直线y=x+b与曲线x=
恰有一个公共点时b的取值范围是-1<b≤1或b=-
,
故选:D.
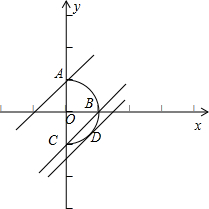 解:曲线x=
解:曲线x=| 1-y2 |
当直线y=x+b经过点A(0,1)时,求得b=1,
当直线y=x+b经过点B(1,0)时,求得b=-1,
当直线和半圆相切于点D时,由圆心O到直线y=x+b的距离等于半径,
可得
| |0-0+b| | ||
|
| 2 |
| 2 |
故当直线y=x+b与曲线x=
| 1-y2 |
| 2 |
故选:D.
点评:本题主要考查了直线与圆相交的性质.对于此类问题除了用联立方程转化为方程的根的问题之外,也可用数形结合的方法较为直观,属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
对正整数n,有抛物线y2=2(2n-1)x,过P(2n,0)任作直线l交抛物线于An,Bn两点,设数列{an}中,a1=-4,且an=
(其中n>1,n∈N),则数列{an}的前n项和Tn=( )
| ||||
| n-1 |
| A、4n |
| B、-4n |
| C、2n(n+1) |
| D、-2n(n+1) |
 如图,△BCD所在的平面垂直于正三角形ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点.
如图,△BCD所在的平面垂直于正三角形ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点.