题目内容
12.直线l:ax+by-3a=0与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}$=1只有一个公共点,则l共有3条,它们的方程是x=3或y=±$\frac{2}{3}$(x-3).分析 直线l:ax+by-3a=0过(3,0),双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}$=1的顶点是(±3,0),渐近线方程为y=±$\frac{2}{3}$x,利用直线l:ax+by-3a=0与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}$=1只有一个公共点,即可得出结论.
解答 解:直线l:ax+by-3a=0过(3,0),双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}$=1的顶点是(±3,0),渐近线方程为y=±$\frac{2}{3}$x
∵直线l:ax+by-3a=0与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}$=1只有一个公共点,
∴直线l的方程为x=3或y=±$\frac{2}{3}$(x-3).
故答案为:3;x=3或y=±$\frac{2}{3}$(x-3).
点评 本题考查直线与双曲线的位置关系,确定直线过定点是关键.

练习册系列答案
相关题目
3.已知数列{an}中,a1=1,an+1=an(1-nan+1),则数列{an}的通项公式为( )
| A. | an=$\frac{{n}^{2}-n+2}{2}$ | B. | an=$\frac{{n}^{2}-n+1}{2}$ | C. | an=$\frac{2}{{n}^{2}-n+1}$ | D. | an=$\frac{2}{{n}^{2}-n+2}$ |
2.在△ABC中,AB=2$\sqrt{3}$,BC=3,∠ABC=30°,则AC=( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{21-6\sqrt{3}}$ | D. | 3 |
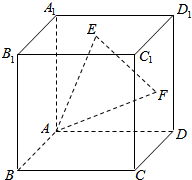 如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:
如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量: