题目内容

5．底面为正方形的四棱锥，其一条测棱垂直于底面，则该四棱锥的三视图可以是下列各图中的（　　）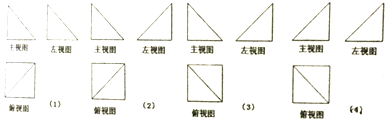
A．（1）（3）B．（1）（4）C．（2）（3）D．（2）（4）

分析 正确画出几何体的三视图，容易判断选项．

解答 解：由题意该四棱锥的直观图如下图所示：

则其三视图如图：
，
故选：D．

点评 本题考查简单几何体的三视图，考查空间想象能力，是基础题．

练习册系列答案
相关题目
15．已知f（x）=cos（ωx+φ）（ω＞0），f'（x）是f（x）的导函数，若f（α）=0，f'（α）＞0，且f（x）在[α，π+α）上没有最小值，则ω的取值范围是（　　）
A．$（0，\frac{1}{2}）$B．$（0，\frac{3}{2}]$C．$（1，\frac{3}{2}]$D．（1，+∞）
16．在钝角△ABC中，a、b、c分别为角A、B、C的对边，已知面积S=$\frac{1}{2}，AB=1，BC=\sqrt{2}$，则AC=（　　）
A．5B．$\sqrt{5}$C．2D．1
13．函数y=loga（x-2）+3（a＞0，a≠1）的图象恒过一定点（3，3）．
20．已知函数f（x）=Asin（ωx+φ）+B，其中A、B、ω、φ均为实数，且A＞0，ω＞0，|φ|＜$\frac{π}{2}$，写出满足f（1）=2，$f（2）=\frac{1}{2}$，f（3）=-1，f（4）=2的一个函数f（x）=$\sqrt{3}$sin（$\frac{2π}{3}$x-$\frac{π}{3}$）+$\frac{1}{2}$（写出一个即可）
10．已知△ABC的内角A、B、C的对边分别为a，b，c．若a=2，c=2$\sqrt{3}$，A=30°，且b＜c，则b=（　　）
A．$\sqrt{3}$B．2$\sqrt{2}$C．2D．2或4
17．已知函数f（x）=ax+lnx，其中a∈R．
（Ⅰ）若f（x）在区间[1，2]上为增函数，求a的取值范围；
（Ⅱ）当a=-e时，证明：f（x）+2≤0；
（Ⅲ）当a=-e时，试判断方程|f（x）|=$\frac{lnx}{x}$+$\frac{3}{2}$是否有实数解，并说明理由．
14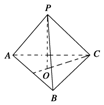．已知点P是正三角形ABC所在平面外一点，PA=PB=PC=$\frac{2}{3}$，AB=1，则PC和平面ABC所成的角是（　　）
A．90°B．60°C．45°D．30°
15．下列叙述中，正确的是（　　）
A．$\overrightarrow{AB}$+$\overrightarrow{BA}$=$\overrightarrow{0}$
B．若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$=$\overrightarrow{b}$
C．若|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|，则$\overrightarrow{a}$⊥$\overrightarrow{b}$
D．若向量$\overrightarrow{b}$与向量$\overrightarrow{a}$共线，则有且只有一个实数λ，使得$\overrightarrow{b}$=λ$\overrightarrow{a}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网