题目内容
10.已知△ABC的内角A、B、C的对边分别为a,b,c.若a=2,c=2$\sqrt{3}$,A=30°,且b<c,则b=( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 2或4 |
分析 利用余弦定理即可得出.
解答 解:∵a=2,c=2$\sqrt{3}$,A=30°,
∴22=b2+$(2\sqrt{3})^{2}$-$4\sqrt{3}b$cos30°,
化为:b2-6b+8=0,且b<c,
则b=2.
故选:C.
点评 本题考查了余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.底面为正方形的四棱锥,其一条测棱垂直于底面,则该四棱锥的三视图可以是下列各图中的( )
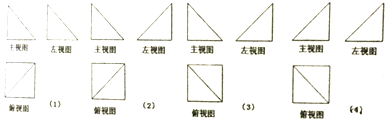

| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
19.“log2x<1”是“x2<x”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |