题目内容
5.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$-$\overrightarrow{b}$=($\sqrt{3}$,$\sqrt{2}$),则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{17}$ | C. | $\sqrt{15}$ | D. | 2$\sqrt{5}$ |
分析 首先求出对$\overrightarrow{a}$-$\overrightarrow{b}$=($\sqrt{3}$,$\sqrt{2}$)平方,求向量$\overrightarrow{a}$,$\overrightarrow{b}$的数量积,然后对|2$\overrightarrow{a}$+$\overrightarrow{b}$|平方,代入两个向量的模长以及数量积求值,然后开方求模长.
解答 解:因为向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$-$\overrightarrow{b}$=($\sqrt{3}$,$\sqrt{2}$),
所以$(\overrightarrow{a}-\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}=5$,所以$\overrightarrow{a}•\overrightarrow{b}$=0,则|2$\overrightarrow{a}$+$\overrightarrow{b}$|2=4${\overrightarrow{a}}^{2}$$+{\overrightarrow{b}}^{2}$$+4\overrightarrow{a}•\overrightarrow{b}$=8,
所以|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{8}$=2$\sqrt{2}$;
故选:A.
点评 本题考查了平面向量模长运算以及数量积的运算;向量的平方与其模长平方相等在求向量模长时经常用到.

 名校课堂系列答案
名校课堂系列答案| A. | (?p)∧q | B. | p∧q | C. | p∧(?q) | D. | p∨(?q) |
 中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
| 45岁以下 | 45岁以上 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率;
②记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 30° | B. | $-\frac{3}{4}$ | C. | $\frac{{10\sqrt{3}}}{3}$ | D. | $5\sqrt{2}$ |
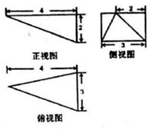 某几何体的三视图如图所示,则该几何体中最长的棱长为( )
某几何体的三视图如图所示,则该几何体中最长的棱长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{21}$ | D. | 2$\sqrt{5}$ |
 如图,四边形ABCD是正方形,四边形ABEG是平行四边形,且平面ABCD⊥平面ABEG,AE⊥AB,EF⊥AG于F,设线段CD、AE的中点分别为P、M.
如图,四边形ABCD是正方形,四边形ABEG是平行四边形,且平面ABCD⊥平面ABEG,AE⊥AB,EF⊥AG于F,设线段CD、AE的中点分别为P、M. 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2