题目内容
要从12个人中选出5人去开会,按下列要求,分别有多少种不同的选法:
(1)甲乙丙三人必须入选;
(2)丁一人不能入选;
(3)甲乙丙三人只有一人入选;
(4)甲乙丙三人至少有一人入选.
(1)甲乙丙三人必须入选;
(2)丁一人不能入选;
(3)甲乙丙三人只有一人入选;
(4)甲乙丙三人至少有一人入选.
考点:古典概型及其概率计算公式
专题:排列组合
分析:由条阿金利用排列组合、两个基本原理的知识求得满足条件的选法数.
解答:
解:(1)∵从12个人中选出5人去开会,甲乙丙三人必须入选,故只需从剩余的9人中再选出2人即可,则有
=36种方法;
(2)若丁一人不能入选,则从其余的11个人中选5个人,方法有
=462种方法;
(3)若甲乙丙三人只有一人入选,则还需从其余的9个人中选4个人,方法有
•
=378种方法;
(4)若甲乙丙三人至少有一入选,则从所有的方法数中减去甲乙丙没有人入选的方法数,即
-
=6336-126=6210种.
| C | 2 9 |
(2)若丁一人不能入选,则从其余的11个人中选5个人,方法有
| C | 5 11 |
(3)若甲乙丙三人只有一人入选,则还需从其余的9个人中选4个人,方法有
| C | 1 3 |
| C | 4 9 |
(4)若甲乙丙三人至少有一入选,则从所有的方法数中减去甲乙丙没有人入选的方法数,即
| C | 5 12 |
| C | 5 9 |
点评:本题主要考查排列组合、两个基本原理的实际应用,体现了分类讨论、转化的数学思想,属于基础题.

练习册系列答案
相关题目
f(x)=
的值域是( )
| 3x+1 |
| 3x+1 |
| A、(3,+∞) |
| B、(0,3) |
| C、(0,2) |
| D、(2,+∞) |
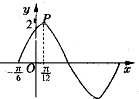 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,