题目内容
15.在Rt△ABC中,∠ACB=90°,$\overrightarrow{BD}$=$\overrightarrow{DA}$,$\overrightarrow{AB}$=2$\overrightarrow{BE}$,则 $\overrightarrow{CD}•\overrightarrow{CA}+\overrightarrow{CE}•\overrightarrow{CA}$=0.分析 由已知画出图形,把$\overrightarrow{CD}、\overrightarrow{CE}$转化为含有$\overrightarrow{CB}、\overrightarrow{CA}$的式子求解.
解答 解:如图,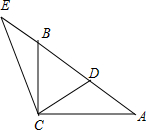
∵∠ACB=90°,$\overrightarrow{BD}$=$\overrightarrow{DA}$,$\overrightarrow{AB}$=2$\overrightarrow{BE}$,
则 $\overrightarrow{CD}•\overrightarrow{CA}+\overrightarrow{CE}•\overrightarrow{CA}$=$(\overrightarrow{CD}+\overrightarrow{CE})•\overrightarrow{CA}$
=$\frac{1}{2}\overrightarrow{CB}•\overrightarrow{CA}=0$.
故答案为:0.
点评 本题考查平面向量的数量积运算,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知某三棱锥的三视图如图所示,则该三棱锥外接球的表面积是( )


| A. | 36π | B. | 24π | C. | 12π | D. | 6π |
7.已知命题p:若x>y,则${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$;命题q:若m>1,则函数 y=x2+mx+1有两个零点.在下列命题中:(1)p∧q;(2)p∨q;(3)p∧(¬q);(4)(¬p)∨q,为真命题的是( )
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
5.复数(1+i)z=1-i(其中i为虚数单位),则z2等于( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
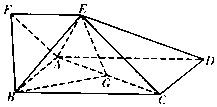 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.