题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x},(x≤1)}\\{lo{g}_{\frac{1}{3}}x,(x>1)}\end{array}\right.$,则函数 y=f (1-x) 的大致图象是( )| A. | 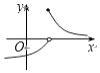 | B. | 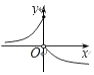 | C. | 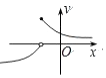 | D. | 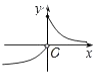 |
分析 利用所求函数图象上的点与函数值的对应关系判断即可.
解答 解:函数 y=f (1-x) 的点为:(0,f(1)),即(0,3)在函数的图象上,排除A,C选项;
函数 y=f (1-x) 的点为:(1,f(0)),即(1,1)在函数的图象上,
排除B,
故选:D.
点评 本题考查函数的图象的判断与应用,充分了解函数的解析式是解题的关键.

练习册系列答案
相关题目
10.已知$P:{x^2}-2x<0,Q:\frac{x+3}{x-1}≤0$,若P真Q假,则x的取值范围是( )
| A. | [1,2) | B. | (1,2) | C. | (-∞,-3) | D. | (-∞,-3] |
11.设集合A={x|(x-1)(x-3)<0},B={y|y=2x,x∈[1,2]},则A∩B=( )
| A. | ∅ | B. | (1,3) | C. | [2,3) | D. | (1,4] |
8.按照图如图所示的程序框图执行,若输出结果为s=31,则M处条件是( )


| A. | k<32? | B. | k>32? | C. | k<16? | D. | k>16? |
5.已知集合 A={x|x2-x-2>0},B={x|1≤x≤3},则 A∩B=( )
| A. | [1,3] | B. | (1,3] | C. | [2,3] | D. | (2,3] |
12.一个几何体的三视图如图所示,则该几何体的体积为( )
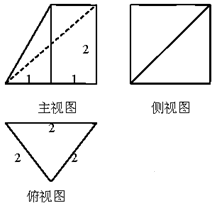

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
10.在平面直角坐标系xoy中,直线l:y=2x-4,圆C的半径为1,圆心在直线l上,若圆C上存在点M,且M在圆D:x2+(y+1)2=4上,则圆心C的横坐标a的取值范围是( )
| A. | $[{\frac{3}{5},2}]$ | B. | $[{0,\frac{12}{5}}]$ | C. | $[{2-\frac{2}{5}\sqrt{5},2+\frac{2}{5}\sqrt{5}}]$ | D. | $[{0,2-\frac{2}{5}\sqrt{5}}]∪[{2+\frac{2}{5}\sqrt{5},4}]$ |