题目内容
3.直角三角形△ABC中,若∠ACB=90°,AC=3,$\overrightarrow{BD}$=2$\overrightarrow{DA}$,$\overrightarrow{AB}$=3$\overrightarrow{BE}$,则 $\overrightarrow{CD}$•$\overrightarrow{CA}$+$\overrightarrow{CE}$•$\overrightarrow{CA}$=3.分析 如图所示,设B(0,a),利用向量的线性运算和数量积运算即可得出.
解答 解:建立如图所示的坐标系,则由题意可得A(3,0) ,C(0,0),设B(0,a).
,C(0,0),设B(0,a).
又∵$\overrightarrow{BD}$=2$\overrightarrow{DA}$,∴$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AD}$=$\overrightarrow{CA}$+$\frac{\overrightarrow{AB}}{3}$=(2,$\frac{a}{3}$);
∵$\overrightarrow{AB}$=3$\overrightarrow{BE}$,∴$\overrightarrow{CE}$=$\overrightarrow{CA}$+$\overrightarrow{AE}$=$\overrightarrow{CA}$+$\frac{4}{3}•\overrightarrow{AB}$=(-1,$\frac{4a}{3}$),
∴$\overrightarrow{CD}$•$\overrightarrow{CA}$+$\overrightarrow{CE}$•$\overrightarrow{CA}$=$\overrightarrow{CA}$•($\overrightarrow{CD}$+$\overrightarrow{CE}$)=(3,0)•(1,$\frac{5a}{3}$)=3,
故答案为:3.
点评 本题考查了向量的线性运算和数量积运算,考查了计算能力,属于基础题.

练习册系列答案
相关题目
14.数列{an}满足a1=1,且an+1=a1+an+n(n∈N*),则$\frac{1}{a_1}+\frac{1}{a_2}+$…$+\frac{1}{{{a_{2016}}}}$等于( )
| A. | $\frac{4032}{2017}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2014}{2015}$ |
11.设集合A={x|(x-1)(x-3)<0},B={y|y=2x,x∈[1,2]},则A∩B=( )
| A. | ∅ | B. | (1,3) | C. | [2,3) | D. | (1,4] |
18.已知△ABC中,$AC=2,AB=2\sqrt{7},cos∠BAC=\frac{{2\sqrt{7}}}{7}$且D是BC的中点,则中线AD的长为( )
| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
8.按照图如图所示的程序框图执行,若输出结果为s=31,则M处条件是( )


| A. | k<32? | B. | k>32? | C. | k<16? | D. | k>16? |
12.一个几何体的三视图如图所示,则该几何体的体积为( )
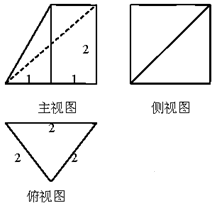

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |