题目内容
函数f（x）=ax-
（a＞0，a≠1）的图象可能是（ ）
| 1 |
| a |
A、 |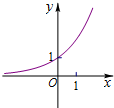
B、 |
C、 |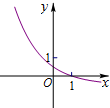
D、 |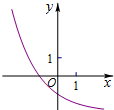
考点：函数的图象
专题：函数的性质及应用
分析：先判断函数的单调性，再判断函数恒经过点（-1，0），问题得以解决．
解答：
解：当0＜a＜1时，函数f（x）=ax-
，为减函数，
当a＞1时，函数f（x）=ax-
，为增函数，
且当x=-1时f（-1）=0，即函数恒经过点（-1，0），
故选：D
| 1 |
| a |
当a＞1时，函数f（x）=ax-
| 1 |
| a |
且当x=-1时f（-1）=0，即函数恒经过点（-1，0），
故选：D
点评：本题主要考查了函数的图象和性质，求出函数恒经过点是关键，属于基础题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
如图中正方体，已知|AG|=|A1G1|，|AH|=|A1H1|，求证：GH∥G1H1，且|GH|=|G1H1|．已知函数f（x）=
，则f（x）在（ ）
| 2x |
| A、（-∞，0）上单调递增 |
| B、（0，+∞）上单调递增 |
| C、（-∞，0）上单调递减 |
| D、（0，+∞）上单调递减 |
设U=R全集，集合A={y|y=x2+1}，B={x|x2-2x-3≥0}，则A∩（∁UB）=（ ）
| A、{x|x≤-1} |
| B、{x|x≤1} |
| C、{x|-1＜x≤1} |
| D、{x|1≤x＜3} |