题目内容
 如图中正方体,已知|AG|=|A1G1|,|AH|=|A1H1|,求证:GH∥G1H1,且|GH|=|G1H1|.
如图中正方体,已知|AG|=|A1G1|,|AH|=|A1H1|,求证:GH∥G1H1,且|GH|=|G1H1|.考点:直线与平面平行的性质,点、线、面间的距离计算
专题:计算题,作图题,空间位置关系与距离
分析:连结GG1,HH1,证明HH1G1G是平行四边形,从而证明GH∥G1H1,且|GH|=|G1H1|.
解答:
 证明:如图,连结GG1,HH1,
证明:如图,连结GG1,HH1,
在正方体中,∵|AG|=|A1G1|,
∴AA1∥GG1,|AA1|=|GG1|;
同理,AA1∥HH1,|AA1|=|HH1|;
∴HH1∥GG1,|HH1|=|GG1|;
∴HH1G1G是平行四边形,
∴GH∥G1H1,且|GH|=|G1H1|.
 证明:如图,连结GG1,HH1,
证明:如图,连结GG1,HH1,在正方体中,∵|AG|=|A1G1|,
∴AA1∥GG1,|AA1|=|GG1|;
同理,AA1∥HH1,|AA1|=|HH1|;
∴HH1∥GG1,|HH1|=|GG1|;
∴HH1G1G是平行四边形,
∴GH∥G1H1,且|GH|=|G1H1|.
点评:本题考查了线线平行的判断证明,同时考查了学生的作图能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=ax-
(a>0,a≠1)的图象可能是( )
| 1 |
| a |
A、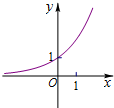 |
B、 |
C、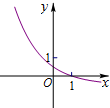 |
D、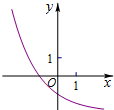 |