题目内容
设a为函数y=2x+arcsinx-
的最大值,则二项式(a
-
)6的展开式中含x2项的系数是 .
| π |
| 2 |
| x |
| 1 | ||
|
考点:二项式定理的应用
专题:计算题,函数的性质及应用,二项式定理
分析:由于函数y=2x+arcsinx-
在[-1,1]上单调递增,即可得到最大值a,再由二项式的通项公式,化简整理,即可得到含x2项的系数.
| π |
| 2 |
解答:
解:由于函数y=2x+arcsinx-
在[-1,1]上单调递增,
则当x=1时,函数取最大值为2+
-
=2,
即a=2.
则二项式(2
-
)6的通项公式:Tr+1=
(2
)6-r(-
)r
=
•26-r•(-1)r•x3-r,
令3-r=2,则r=1.
则含x2项的系数为:
•25•(-1)1=-192.
故答案为:-192.
| π |
| 2 |
则当x=1时,函数取最大值为2+
| π |
| 2 |
| π |
| 2 |
即a=2.
则二项式(2
| x |
| 1 | ||
|
| C | r 6 |
| x |
| 1 | ||
|
=
| C | r 6 |
令3-r=2,则r=1.
则含x2项的系数为:
| C | 1 6 |
故答案为:-192.
点评:本题考查函数的单调性及运用:求最值,考查二项式定理的运用,主要是通项公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=ax-
(a>0,a≠1)的图象可能是( )
| 1 |
| a |
A、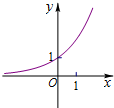 |
B、 |
C、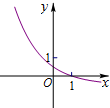 |
D、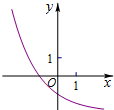 |
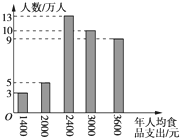 对“小康县”的经济评价标准:
对“小康县”的经济评价标准:①年人均收入不小于7000元;
②年人均食品支出不大于收入的35%.某县有40万人,调查数据如下:
| 年人均收入/元 | 0 | 2000 | 4000 | 6000 | 8000 | 10 000 | 12 000 | 16 000 |
| 人数/万人 | 6 | 3 | 5 | 5 | 6 | 7 | 5 | 3 |
| A、是小康县 |
| B、达到标准①,未达到标准②,不是小康县 |
| C、达到标准②,未达到标准①,不是小康县 |
| D、两个标准都未达到,不是小康县 |
已知集合A=[x|-1≤x<2},B={x|x-a≤0},若A⊆B,则实数a的取值范围是( )
| A、a≤2 | B、a≥-1 |
| C、a>-1 | D、a≥2 |