题目内容
设二次函数f(x)=x2+ax+b.对任意实数x,都存在y,使得f(y)=f(x)+y,则a的最大值是 .
考点:函数恒成立问题
专题:函数的性质及应用
分析:先将原式化成f(y)-y=f(x)的形式,因为对任意实数x,都存在y,使得f(y)-y=f(x),则只需f(x)的值域是函数f(y)-y的值域的子集.则问题容易获解.
解答:
解:由已知得f(x)=x2+ax+b,f(y)=y2+ay+b.
则原式可化为对任意实数x,都存在y使得x2+ax=y2+ay-y恒成立,
令g(x)=x2+ax,h(y)=y2+ay-y,
则函数g(x)=x2+ax的值域是函数h(y)=y2+ay-y值域的子集.
g(x)=(x+
)2-
,值域为[-
,+∞),
h(y)=y2+(a-1)y=[y+(
)]2-
,值域为[-
,+∞),
从而-
≥-
,解得a≤
,
故a的最大值为
.
故答案为
.
则原式可化为对任意实数x,都存在y使得x2+ax=y2+ay-y恒成立,
令g(x)=x2+ax,h(y)=y2+ay-y,
则函数g(x)=x2+ax的值域是函数h(y)=y2+ay-y值域的子集.
g(x)=(x+
| a |
| 2 |
| a2 |
| 4 |
| a2 |
| 4 |
h(y)=y2+(a-1)y=[y+(
| a-1 |
| 2 |
| (a-1)2 |
| 4 |
| (a-1)2 |
| 4 |
从而-
| a2 |
| 4 |
| (a-1)2 |
| 4 |
| 1 |
| 2 |
故a的最大值为
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题重在理解题意,先将变量x与y分离后,即将原式化成两个函数值相等,结合题意即将问题转化为两个函数值域的包含关系.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
函数f(x)=ax-
(a>0,a≠1)的图象可能是( )
| 1 |
| a |
A、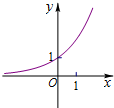 |
B、 |
C、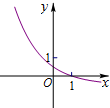 |
D、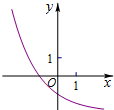 |
原点和点(1,1)在直线x+y=a两侧,则a的取值范围是( )
| A、0<a<2 |
| B、a<0或a>2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
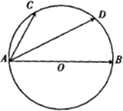
如图,AB是⊙O的直径,点C,D是半圆弧AB上的两个三等分点,
=
,
=
,则
=( )
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
为了得到函数y=31-x的图象,可以把函数y=3-x的图象( )
| A、向左平移3个单位长度 |
| B、向右平移3个单位长度 |
| C、向左平移1个单位长度 |
| D、向右平移1个单位长度 |