题目内容
已知函数f(x)=
,则f(x)在( )
| 2x |
| A、(-∞,0)上单调递增 |
| B、(0,+∞)上单调递增 |
| C、(-∞,0)上单调递减 |
| D、(0,+∞)上单调递减 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据单调函数的定义,利用定义直接证明,或利用导数判断也可以.
解答:
解:∵f(x)=
=
∴x∈[0,+∞),x>0时,f′(x)=
>0,∴f(x)在[0,+∞0上是递增函数.
故选:B
| 2x |
| 2 |
| x |
| ||
| 2x |
故选:B
点评:本题考查函数的单调区间,属于基础题.

练习册系列答案
相关题目
函数f(x)=ax-
(a>0,a≠1)的图象可能是( )
| 1 |
| a |
A、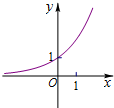 |
B、 |
C、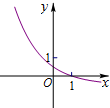 |
D、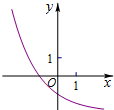 |