题目内容
在平面直角坐标系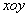 中,已知椭圆
中,已知椭圆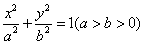 的离心率为
的离心率为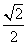 ,其焦点在圆
,其焦点在圆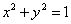 上.
上.
(1)求椭圆的方程;
(2)设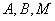 是椭圆上的三点(异于椭圆的顶点),且存在锐角
是椭圆上的三点(异于椭圆的顶点),且存在锐角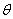 ,使
,使
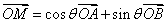 .
.
① 求证:直线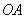 与
与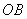 的斜率的乘积为定值;
的斜率的乘积为定值;
② 求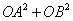 的值.
的值.
(1)根据题意得 ,于是
,于是 ,
,
所以椭圆方程为 .
.
(2)①设 则
则 ,
,
又设 ,由
,由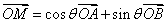 得
得 ,
,
又 在椭圆上,
在椭圆上,
整理得 ,
,
 ,
, .
.
 为定值.
为定值.
②
 ,又
,又 ,
, ,
,
 .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
在平面直角坐标系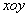 中,已知椭圆
中,已知椭圆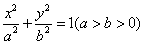 的离心率为
的离心率为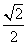 ,其焦点在圆
,其焦点在圆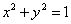 上.
上.
(1)求椭圆的方程;
(2)设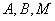 是椭圆上的三点(异于椭圆的顶点),且存在锐角
是椭圆上的三点(异于椭圆的顶点),且存在锐角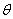 ,使
,使
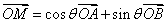 .
.
① 求证:直线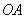 与
与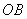 的斜率的乘积为定值;
的斜率的乘积为定值;
② 求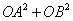 的值.
的值.
(1)根据题意得 ,于是
,于是 ,
,
所以椭圆方程为 .
.
(2)①设 则
则 ,
,
又设 ,由
,由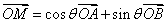 得
得 ,
,
又 在椭圆上,
在椭圆上,
整理得 ,
,
 ,
, .
.
 为定值.
为定值.
②
 ,又
,又 ,
, ,
,
 .
.


 阅读快车系列答案
阅读快车系列答案