题目内容
已知函数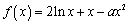 ,
,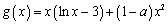 .
.
(1)若函数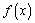 在区间
在区间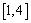 上单调递增,求实数
上单调递增,求实数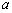 的取值范围;
的取值范围;
(2)若曲线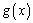 在
在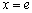 处的切线平行于直线
处的切线平行于直线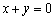 ,求证:
,求证:
对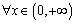 ,
,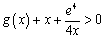 ;
;
(3)设函数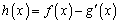 ,试讨论函数
,试讨论函数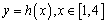 的零点个数.
的零点个数.
(1)由题意,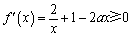 在
在 上恒成立,
上恒成立,
即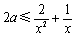 在
在 上恒成立.
上恒成立.
设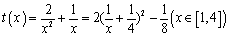 ,所以
,所以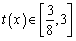 ,
,
所以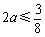 ,即
,即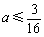 .
.
(2)由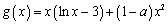 ,得
,得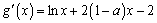 .
.
由题意,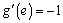 ,即
,即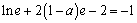 ,所以
,所以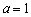 .
.
所以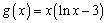 .
.
不等式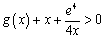 即为
即为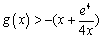 .
.
由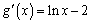 ,知函数
,知函数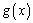 在
在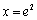 处取最小值为
处取最小值为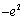 ,
,
设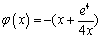 ,因为
,因为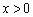 ,所以
,所以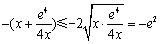 ,
,
当且仅当 时取“=”,即当
时取“=”,即当 时,
时,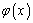 的最大值为
的最大值为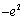 ,
,
因为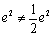 ,所以
,所以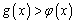 ,即原不等式成立.
,即原不等式成立.
(注:不等式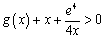 即为
即为 ,
,
设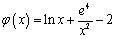 ,证明
,证明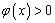 对
对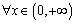 成立,证明略)
成立,证明略)
(3)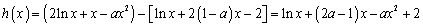 ,
,
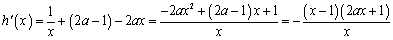 .
.
①当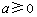 时,由于
时,由于 ,所以
,所以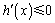 ,所以
,所以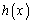 在
在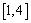 上递减,
上递减,
由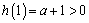 ,
,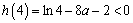 ,所以函数
,所以函数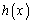 在
在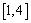 上的零点个数1;
上的零点个数1;
②当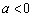 时,
时,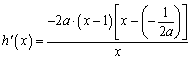 ,
,
 当
当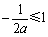 ,即
,即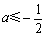 时,当
时,当 时,
时,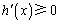 ,所以
,所以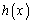 在
在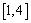 上递增,
上递增,
因为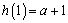 ,
,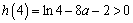 ,
,
所以当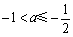 时,函数
时,函数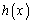 在
在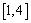 上的零点个数0;
上的零点个数0;
当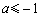 时,函数
时,函数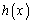 在
在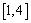 上的零点个数1.
上的零点个数1.
 当
当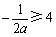 ,即
,即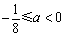 时,
时,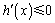 ,所以
,所以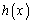 在
在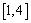 上递减,
上递减,
因为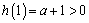 ,
,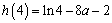 ,
,
所以当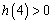 ,即
,即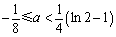 时,函数
时,函数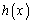 在
在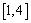 上的零点个数0;
上的零点个数0;
当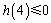 ,即
,即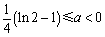 时,函数
时,函数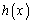 在
在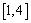 上的零点个数1.
上的零点个数1.
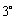 当
当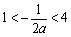 ,即
,即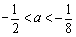 时,
时,
满足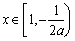 时,
时,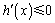 ;
;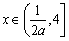 时,
时,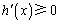 ,
,
即函数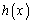 在
在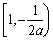 上递减,在
上递减,在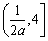 上递增,
上递增,
因为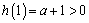 ,
,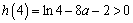 ,
,
而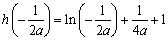 ,
,
设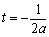 ,则
,则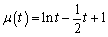 ,且
,且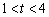 ,
,
由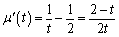 ,知
,知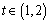 时,
时,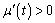 ,
,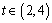 时,
时, ,
,
即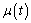 在
在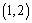 上为增函数,在
上为增函数,在 上为减函数,
上为减函数,
因为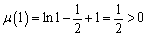 ,
,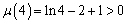 ,
,
所以当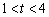 时,
时,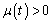 ,即
,即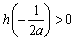 ,
,
所以当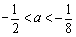 时,函数
时,函数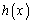 在
在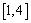 上的零点个数0.
上的零点个数0.
综上所述,当 时,函数
时,函数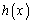 在
在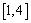 上的零点个数0;
上的零点个数0;
当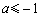 或
或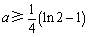 时,函数
时,函数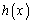 在
在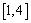 上的零点个数1.
上的零点个数1.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 (
( 为虚数单位),则复数
为虚数单位),则复数 的模为 .
的模为 . 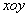 中,已知椭圆
中,已知椭圆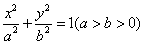 的离心率为
的离心率为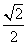 ,其焦点在圆
,其焦点在圆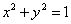 上.
上.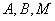 是椭圆上的三点(异于椭圆的顶点),且存在锐角
是椭圆上的三点(异于椭圆的顶点),且存在锐角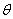 ,使
,使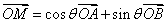 .
.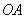 与
与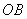 的斜率的乘积为定值;
的斜率的乘积为定值;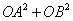 的值.
的值. ]上为增函数,且图象关于点(3π,0)对称,则ω的取值集合为 .
]上为增函数,且图象关于点(3π,0)对称,则ω的取值集合为 .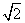 acos B=ccos B+bcos C.
acos B=ccos B+bcos C.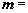 (cos A,cos 2A),
(cos A,cos 2A),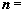 (12,-5),求当
(12,-5),求当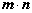 取最大值时,tan C的值.
取最大值时,tan C的值. -
- +
+ -
- +…+
+…+ -
- 的值.
的值.
 (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsin
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsin θ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
θ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长. ,则二项式
,则二项式 的展开式中
的展开式中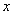 的系数为
的系数为