题目内容
2.在△ABC中,AB=BC=3,∠BAC=30°,CD是AB边上的高,则$\overrightarrow{CD}•\overrightarrow{CB}$=( )| A. | $-\frac{9}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27}{4}$ | D. | $-\frac{27}{4}$ |
分析 利用三角形的知识计算CD,∠BCD,利用平面向量的数量积的定义计算数量积.
解答 解:∵AB=BC=3,∠BAC=30°,CD⊥AB,
∴∠ABC=120°,∠BCD=30°,
∴AC=$\sqrt{{3}^{2}+{3}^{2}-2×3×3×cos120°}$=3$\sqrt{3}$,
∴CD=ACsin∠CAB=$\frac{3\sqrt{3}}{2}$,
∴$\overrightarrow{CD}•\overrightarrow{CB}$=$\frac{3\sqrt{3}}{2}×3×cos30°$=$\frac{27}{4}$.
故选:C.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
13.若g(x)=2x-1,f[g(x)]=$\frac{1+{x}^{2}}{3{x}^{2}}$,则f(-3)=( )
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
7.圆x2+y2=1与直线xsinθ+y-1=0的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相切或相交 |
11.数列{an}的前n项和Sn=n2-5n(n∈N*),若p-q=4,则ap-aq=( )
| A. | 20 | B. | 16 | C. | 12 | D. | 8 |
12.已知直线a,b以及平面α,β,则下列命题正确的是( )
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,b⊥α,则 a⊥b | ||
| C. | 若a∥b,b∥α,则a∥α | D. | 若a⊥α,b∥β,则 α⊥β |
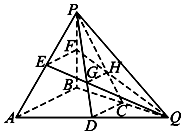 如图所示,在三棱锥PABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH.求证:
如图所示,在三棱锥PABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH.求证: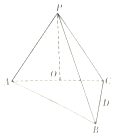 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.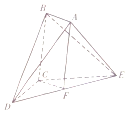 在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.
在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.