题目内容
12.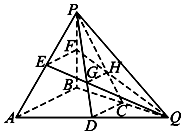 如图所示,在三棱锥PABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH.求证:
如图所示,在三棱锥PABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH.求证:(1)求证:AB∥GH.
(2)若三棱锥P-ABQ为正四面体,且棱长为2,求多面体ADGE-BCHF的体积.
分析 (1)推导出EF∥AB,DC∥AB.从而EF∥DC.进而EF∥平面PCD.再求出EF∥GH,由此能证明AB∥GH.
(2)设正四面体三棱锥P-ABQ的体积为V,由${V_{ADGE-BCHF}}=V-\frac{1}{4}V-\frac{5}{36}V$,能求出多面体ADGE-BCHF的体积.
解答 证明:(1)∵D,C,E,F分别是AQ,BQ,AP,BP的中点,
∴EF∥AB,DC∥AB.∴EF∥DC.
又EF?平面PCD,DC?平面PCD,
∴EF∥平面PCD.
又EF?平面EFQ,平面EFQ∩平面PCD=GH,
∴EF∥GH.又EF∥AB,∴AB∥GH.
解:(2)设正四面体三棱锥P-ABQ的体积为V,
则V=$\frac{1}{3}×(\frac{1}{2}×2×2×sin60°)$×$\sqrt{{2}^{2}-(\frac{2}{3}\sqrt{{2}^{2}-{1}^{2}})^{2}}$=$\frac{2\sqrt{2}}{3}$,
∵${V_{P-EFQ}}=\frac{1}{4}V,{V_{Q-CDGH}}=\frac{5}{36}V$,
∴${V_{ADGE-BCHF}}=V-\frac{1}{4}V-\frac{5}{36}V=\frac{11}{18}V=\frac{{11\sqrt{2}}}{27}$.
点评 本题考查线面垂直的证明,考查两个三棱锥的体积之比的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在△ABC中,AB=BC=3,∠BAC=30°,CD是AB边上的高,则$\overrightarrow{CD}•\overrightarrow{CB}$=( )
| A. | $-\frac{9}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27}{4}$ | D. | $-\frac{27}{4}$ |
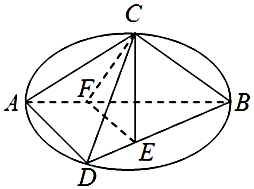 如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.