题目内容
12.已知直线a,b以及平面α,β,则下列命题正确的是( )| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,b⊥α,则 a⊥b | ||
| C. | 若a∥b,b∥α,则a∥α | D. | 若a⊥α,b∥β,则 α⊥β |
分析 对4个命题分别进行判断,即可得出结论.
解答 解:对于A,若a∥α,b∥α,则a∥b或a,b相交、异面,不正确;
对于B,若a∥α,则经过a的平面与α交于c,a∥c,∵b⊥α,∴b⊥c,∵a∥c,∴a⊥b,正确;
对于C,若a∥b,b∥α,则a∥α或a?α,不正确;
对于D,若a⊥α,b∥β,则α、β位置关系不确定,不正确,
故选B.
点评 本题考查了空间线面、面面位置关系、简易逻辑的判定方法,考查了推理能力,属于中档题.

练习册系列答案
相关题目
2.在△ABC中,AB=BC=3,∠BAC=30°,CD是AB边上的高,则$\overrightarrow{CD}•\overrightarrow{CB}$=( )
| A. | $-\frac{9}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27}{4}$ | D. | $-\frac{27}{4}$ |
3.下列说法正确的是( )
| A. | 若x,y∈R,且$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,则$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$ | |
| B. | 设命题p:?x>0,x2>2x,则¬p:?x0≤0,x02≤2${\;}^{{x}_{0}}$ | |
| C. | △ABC中,A>B是sinA>sinB的充分必要条件 | |
| D. | 命题“若a=-1,则f(x)=ax2+2x-1只有一个零点”的逆命题为真 |
20.已知点F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,点B是短轴顶点,直线BF2与椭圆C相交于另一点D.若△F1BD是等腰三角形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
4.已知$\overrightarrow{a}$,$\overrightarrow{b}$是两个向量,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,若在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,D为BC中点,则AD的长为( )
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
2.抛物线y=$\frac{1}{4}$x2的准线方程是( )
| A. | y=-1 | B. | y=1 | C. | x=-$\frac{1}{16}$ | D. | x=$\frac{1}{16}$ |
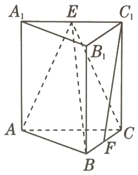 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.