题目内容
7．圆x2+y2=1与直线xsinθ+y-1=0的位置关系为（ ）| A． | 相交 | B． | 相切 | C． | 相离 | D． | 相切或相交 |
分析 求出圆心坐标和半径r，求出直线系经过的定点，判断定点与圆的位置关系，可得出直线与圆位置关系．
解答 解：由圆的标准方程：x2+y2=1，
∴圆心坐标为（0，0），半径r=1，
∵直线xsinα+y-1=0，恒过（0，1），而（0，1）是圆周上的点．
∴直线与圆的位置关系是相交或相切．
故选D．
点评 此题考查了直线与圆的位置关系，涉及的知识有：圆的标准方程，点到直线的距离公式，以及正弦函数的值域，直线与圆的位置关系由d与r的大小关系确定（d表示圆心到直线的距离，r表示圆的半径），当d＞r时，直线与圆相离；当d=r时，直线与圆相切；当d＜r时，直线与圆相交．本题是直线系与圆的位置关系，转化为点与圆的位置关系判断．
练习册系列答案
名校课堂系列答案
相关题目
18．对于平面α和两条不同的直线m、n，下列命题是真命题的是（ ）
| A． | 若m，n与α所成的角相等，则m∥n | B． | 若m∥α，n∥α，则m∥n | ||
| C． | 若m⊥α，m⊥n，则n∥α | D． | 若m⊥α，n⊥α，则m∥n |
15．设等比数列{an}的公比为q，前n项和为Sn，且a1＞0，若S2＞2a3，则q的取值范围是（ ）
| A． | $（-1，0）∪（0，\frac{1}{2}）$ | B． | $（-\frac{1}{2}，0）∪（0，1）$ | C． | $（-1，\frac{1}{2}）$ | D． | $（-\frac{1}{2}，1）$ |
2．在△ABC中，AB=BC=3，∠BAC=30°，CD是AB边上的高，则$\overrightarrow{CD}•\overrightarrow{CB}$=（ ）
| A． | $-\frac{9}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{27}{4}$ | D． | $-\frac{27}{4}$ |
12．30岁以后，随着年龄的增长，人们的身体机能在逐渐退化，所以打针 买保健品这样的“健康消费”会越来越多，现对某地区不同年龄段的一些人进行了调查，得到其一年内平均“健康消费”如表：
（1）求“健康消费”y关于年龄x的线性回归方程；
（2）由（1）所得方程，估计该地区的人在60岁时的平均“健康消费”．
（附：线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中，$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，其中$\overline{x}$，$\overline{y}$为样本平均值）
| 年龄（岁） | 30 | 35 | 40 | 45 | 50 |
| 健康消费（百元） | 5 | 8 | 10 | 14 | 18 |
（2）由（1）所得方程，估计该地区的人在60岁时的平均“健康消费”．
（附：线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中，$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，其中$\overline{x}$，$\overline{y}$为样本平均值）
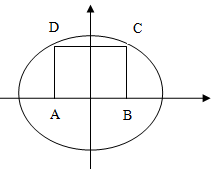如图，长为2$\sqrt{3}$，宽为$\frac{1}{2}$的矩形ABCD，以A、B为焦点的椭圆M：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点．