题目内容
10.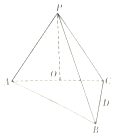 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O为AC中点,D是BC上一点,OP⊥底面ABC,BC⊥面POD.(Ⅰ)求证:点D为BC中点;
(Ⅱ)当k取何值时,O在平面PBC内的射影恰好是PD的中点.
分析 (Ⅰ)由BC⊥平面POD得BC⊥OD,由AB⊥BC得OD∥AB,再由O为AC中点得点D为BC的中点;
(Ⅱ)作OF⊥PD于点F,证明OF⊥平面PBC,PO=OD,利用勾股定理PA2=PO2+OA2,列方程求出k的值.
解答 解:(Ⅰ)证明:由BC⊥平面POD,得BC⊥OD,
又AB⊥BC,则OD∥AB,
又O为AC中点,所以点D为BC的中点,…(6分)
(Ⅱ)如图,
过O作OF⊥PD于点F,
由OF⊥PD,OF⊥BC,PD∩BC=D,
∴OF⊥平面PBC,
又F为PD的中点,∴△POD为等腰三角形,
∴PO=OD,
不妨设PA=x,则AB=kx,PO=OD=$\frac{1}{2}$kx,AO=$\frac{\sqrt{2}}{2}$kx,
在Rt△POA中,PA2=PO2+OA2,
代入解得k=$\frac{2\sqrt{3}}{3}$.…(12分).
点评 本题考查了空间中的垂直与平行关系的应用问题,也考查了证明与计算问题,是综合性题目.

练习册系列答案
相关题目
18.对于平面α和两条不同的直线m、n,下列命题是真命题的是( )
| A. | 若m,n与α所成的角相等,则m∥n | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m⊥α,m⊥n,则n∥α | D. | 若m⊥α,n⊥α,则m∥n |
15.设等比数列{an}的公比为q,前n项和为Sn,且a1>0,若S2>2a3,则q的取值范围是( )
| A. | $(-1,0)∪(0,\frac{1}{2})$ | B. | $(-\frac{1}{2},0)∪(0,1)$ | C. | $(-1,\frac{1}{2})$ | D. | $(-\frac{1}{2},1)$ |
2.在△ABC中,AB=BC=3,∠BAC=30°,CD是AB边上的高,则$\overrightarrow{CD}•\overrightarrow{CB}$=( )
| A. | $-\frac{9}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27}{4}$ | D. | $-\frac{27}{4}$ |
20.已知点F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,点B是短轴顶点,直线BF2与椭圆C相交于另一点D.若△F1BD是等腰三角形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |