题目内容
11.数列{an}的前n项和Sn=n2-5n(n∈N*),若p-q=4,则ap-aq=( )| A. | 20 | B. | 16 | C. | 12 | D. | 8 |
分析 根据an=Sn-Sn-1可得an是等差数列,可得答案.
解答 解:Sn=n2-5n(n∈N*),可得a1=Sn=-4
当n≥2时,则Sn-1=(n-1)2-5(n-1)=n2+7n+6.
∵an=Sn-Sn-1
∴an=2n-6,
当n=1,可得a1=-4
∵an-an-1=2常数,∴an是等差数列,首项为-4,公差d=2.
∵p-q=4,
令q=1,则p=5,
那么a5-a1=8.
故选D
点评 本题考查等差的证明与等差数列的性质的运用,考查运算与推理,属于基础题.

练习册系列答案
相关题目
2.在△ABC中,AB=BC=3,∠BAC=30°,CD是AB边上的高,则$\overrightarrow{CD}•\overrightarrow{CB}$=( )
| A. | $-\frac{9}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27}{4}$ | D. | $-\frac{27}{4}$ |
6.下列四个函数中,既是奇函数又在定义域上单调递减的是( )
| A. | y=2-|x| | B. | y=tanx | C. | y=-x3 | D. | $y={log_{\frac{1}{5}}}x$ |
3.下列说法正确的是( )
| A. | 若x,y∈R,且$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,则$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$ | |
| B. | 设命题p:?x>0,x2>2x,则¬p:?x0≤0,x02≤2${\;}^{{x}_{0}}$ | |
| C. | △ABC中,A>B是sinA>sinB的充分必要条件 | |
| D. | 命题“若a=-1,则f(x)=ax2+2x-1只有一个零点”的逆命题为真 |
20.已知点F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,点B是短轴顶点,直线BF2与椭圆C相交于另一点D.若△F1BD是等腰三角形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
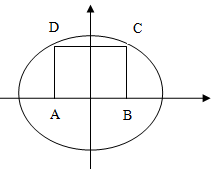 如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.
如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.