题目内容
14.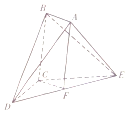 在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.
在如图所示的多面体ABCDE中,四边形ABCF为平行四边形,F为DE的中点,△BCE为等腰直角三角形,BE为斜边,△BDE为正三角形,CD=CE=2.(1)证明:CD⊥BE;
(2)求四面体ABDE的体积.
分析 (1)由△BCE为等腰直角三角形,BE为斜边,可得CB=CE=2,BE=2$\sqrt{2}$,从而求得BD=2$\sqrt{2}$,然后利用勾股定理可得CD⊥BC,同理,可得CD⊥CE.再由线面垂直的判定可得CD⊥平面BCE,进一步得到CD⊥BE;
(2)又(1)可得BC⊥平面DCE,由四边形ABCF为平行四边形,可得AF⊥平面DCE,得到AF⊥DE,再由CD=CE,F为DE的中点,得CF⊥DE,进一步得到DE⊥平面ABCF.然后利用VA-BDE=VD-ABF+VE-ABF=$\frac{1}{3}{S}_{△ABF}•DE$求得四面体ABDE的体积.
解答 (1)证明:∵△BCE为等腰直角三角形,BE为斜边,∴CB=CE=2,BE=2$\sqrt{2}$.
∵△BDE为正三角形,∴BD=2$\sqrt{2}$,
在三角形BDC中,BC2+CD2=BD2,∴CD⊥BC,
同理,可得CD⊥CE.
∵BC∩CE=C,∴CD⊥平面BCE,
又BE?平面BCE,∴CD⊥BE;
(2)又(1)可得BC⊥平面DCE,
∵四边形ABCF为平行四边形,∴AF⊥平面DCE,则AF⊥DE,
又CD=CE,F为DE的中点,∴CF⊥DE,
又CF∩AF=F,∴DE⊥平面ABCF.
连接BF,则VA-BDE=VD-ABF+VE-ABF=$\frac{1}{3}{S}_{△ABF}•DE$
=$\frac{1}{3}•\frac{1}{2}•2•\sqrt{2}•2\sqrt{2}=\frac{4}{3}$.
∴四面体ABDE的体积为$\frac{4}{3}$.
点评 本题考查线面垂直的判定和性质,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
2.在△ABC中,AB=BC=3,∠BAC=30°,CD是AB边上的高,则$\overrightarrow{CD}•\overrightarrow{CB}$=( )
| A. | $-\frac{9}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{27}{4}$ | D. | $-\frac{27}{4}$ |
6.下列四个函数中,既是奇函数又在定义域上单调递减的是( )
| A. | y=2-|x| | B. | y=tanx | C. | y=-x3 | D. | $y={log_{\frac{1}{5}}}x$ |
3.下列说法正确的是( )
| A. | 若x,y∈R,且$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,则$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$ | |
| B. | 设命题p:?x>0,x2>2x,则¬p:?x0≤0,x02≤2${\;}^{{x}_{0}}$ | |
| C. | △ABC中,A>B是sinA>sinB的充分必要条件 | |
| D. | 命题“若a=-1,则f(x)=ax2+2x-1只有一个零点”的逆命题为真 |
4.已知$\overrightarrow{a}$,$\overrightarrow{b}$是两个向量,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,若在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,D为BC中点,则AD的长为( )
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |