题目内容

已知-7，a1，a2，-1四个实数成等差数列，-4，b1，b2，b3，-1五个实数成等比数列，则
a2-a1
b2
=
 
．
考点：等比数列的性质
专题：等差数列与等比数列
分析：设公差为d，公比为q，由题意可解得d和q2，代入要求的式子化简可得．
解答： 解：设等差数列的公差为d，等比数列的公比为q，
则有-7+3d=-1，-4•q4=-1，
解得d=2，q2=
1
2
，
∴
a2-a1
b2
=
d
-4q2
=
2
-4×
1
2
=-1．
故答案为：-1
点评：本题考查等比数列和等差数列的性质和应用，属基础题．
练习册系列答案
相关题目
设F1，F2是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右两个焦点，若双曲线C上存在点P满足|PF1|：|PF2|=2：1且∠F1PF2=90°，则双曲线C的渐近线方程是（　　）
A、x±2y=0
B、2x±y=0
C、5x±4y=0
D、4x±5y=0
已知函数f（x）=ax（a＞0，a≠1），且f（-2）=
1
4
．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设函数g（x）=log2[m-f2（x）+4f（x）]若此函数在[0，2]上存在零点，求实数m的取值范围；
（Ⅲ）若
1
3
≤k＜1，函数f1（x）=|f（x）-1|-k的零点分别为x1，x2（x1＜x2），函数f2（x）=|f（x）-1|-
k
2k+1
的零点分别为x3，x4（x3＜x4），求x1-x2+x3-x4的最大值．
我国高铁技术发展迅速，铁道部门计划在A，B两城市之间开通高速列车，假设列车在试运行期间，每天在8：00～9：00，9：00～10：00两个时间段内各发一趟由A城开往B城的列车（两车发车情况互不影响），A城发车时间及概率如下表所示：
发车时间8：108：308：509：109：309：50
概率
1
6
1
3
1
2
1
6
1
3
1
2
若甲、乙两位旅客打算从A城到B城，他们到达A城火车站的时间分别是周六的8：00和周日的8：20．（只考虑候车时间，不考虑其他因素）
（1）求甲、乙两人候车时间相等的概率；
（2）设乙候车所需时间为随机变量X，求ξ的分布列和数学期望E（X）．
在数列{an}中，a1=1，an+1=
an
1+an
（n=1，2，3，…），
（1）计算a1，a2，a3，a4；
（2）猜想an的表达式，并用数学归纳法证明你的结论．
已知直线l经过两条直线l1：x+y-4=0和l2：x-y+2=0的交点，直线l3：2x-y-1=0；
（1）若l∥l3，求l的直线方程；
（2）若l⊥l3，求l的直线方程．
已知圆C1：（x-1）2+（y-1）2=2与圆C2关于直线l：y=x+m对称．
（1）若直线l截圆C1所得弦长为2，求实数m的值；
（2）若m=4，P为直线l上一动点，过P作圆C2的两条切线，切点分别为A，B，求
PA
•
PB
的取值范围．
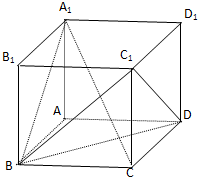如图，正方体ABCD-A1B1C1D1的棱长为1．
（1）求异面直线BA1与CC1所成角的大小；
（2）求证：A1C⊥平面BC1D；
（3）求三棱锥C-BDC1的表面积．
设集合A=（-∞，a]，B=（b，+∞），a∈N，b∈R，且A∩B∩N={2}，则a+b的取值区间是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网