题目内容
某公司在统计2012年的经营状况时发现,若不考虑其他因素,该公司每月获得的利润y(万元)与月份之间满足函数关系式:f(x)=
(Ⅰ)求该公司5月份获得的利润为多少万元?
(Ⅱ)2012年该公司哪个月的月利润最大?最大值是多少万元?
|
(Ⅰ)求该公司5月份获得的利润为多少万元?
(Ⅱ)2012年该公司哪个月的月利润最大?最大值是多少万元?
考点:二分法求方程的近似解
专题:函数的性质及应用
分析:(I)由已知中的函数解析式,装饰x=5代入可得答案.
(II)分析函数的单调性,求出各段上的最大值,比较后,可得答案.
(II)分析函数的单调性,求出各段上的最大值,比较后,可得答案.
解答:
解:(Ⅰ)∵f(x)=
,
∴当x=5时,f(x)=12x+28=12×5+28=88,
所以该公司5月份获得的利润为88万元.
(Ⅱ)因为f(x)=12x+28(1≤x≤6,x∈N*),单调递增,
当x=6时,f(6)=100;
f(x)=200-14x(6<x≤12,x∈N*),单调递减,
当x=7时,f(7)=102,
所以2012年该公司7月份的月利润最大,最大值为102万.
|
∴当x=5时,f(x)=12x+28=12×5+28=88,
所以该公司5月份获得的利润为88万元.
(Ⅱ)因为f(x)=12x+28(1≤x≤6,x∈N*),单调递增,
当x=6时,f(6)=100;
f(x)=200-14x(6<x≤12,x∈N*),单调递减,
当x=7时,f(7)=102,
所以2012年该公司7月份的月利润最大,最大值为102万.
点评:本题考查的知识点是分段函数,函数求值,函数的最值,难度不大,属于基础题.

练习册系列答案
相关题目
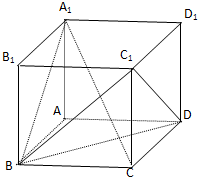 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.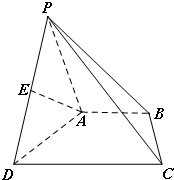 如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱
如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱