题目内容
画出正弦函数y=sinx,(x∈R)的简图,并根据图象写出-
≤y≤
时x的集合.
| 1 |
| 2 |
| ||
| 2 |
考点:五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:先作简图,然后观察在哪些区域能使不等式成立,即可得到结论.
解答:
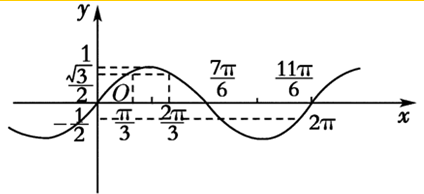 解:在周期[-
解:在周期[-
,
]内,当y=-
时,x=-
或
,
当y=
,得x=
或
,
此时满足不等式-
≤y≤
的解为-
≤x≤
或
≤x≤
,
∵函数的周期是2kπ,k∈Z,
∴不等式的解为-
+2kπ≤x≤
+2kπ,或
+2kπ≤x≤
+2kπ,
故不等式的解集为{x|-
+2kπ≤x≤
+2kπ,或
+2kπ≤x≤
+2kπ},k∈Z.
 解:在周期[-
解:在周期[-| π |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
当y=
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
此时满足不等式-
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| 7π |
| 6 |
∵函数的周期是2kπ,k∈Z,
∴不等式的解为-
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| 7π |
| 6 |
故不等式的解集为{x|-
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| 7π |
| 6 |
点评:本题主要考查三角函数的图象性质,以及三角函数对应不等式的求解,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
设F1,F2是双曲线C:
-
=1(a>0,b>0)的左、右两个焦点,若双曲线C上存在点P满足|PF1|:|PF2|=2:1且∠F1PF2=90°,则双曲线C的渐近线方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、x±2y=0 |
| B、2x±y=0 |
| C、5x±4y=0 |
| D、4x±5y=0 |
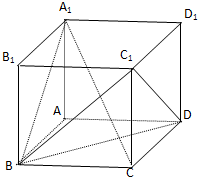 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.