题目内容
工商部门对甲、乙两家食品加工企业的产品进行深入检查后,决定对甲企业的5种产品和乙企业的3种产品做进一步的检验.检验员从以上8种产品中每次抽取一种逐一不重复地进行化验检验.
(Ⅰ)求前3次检验的产品中至少1种是乙企业的产品的概率;
(Ⅱ)记检验到第一种甲企业的产品时所检验的产品种数共为X,求X的分布列和数学期望.
(Ⅰ)求前3次检验的产品中至少1种是乙企业的产品的概率;
(Ⅱ)记检验到第一种甲企业的产品时所检验的产品种数共为X,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)利用对立事件的概率公式能求出前3次检验的产品中至少1种是乙企业的产品的概率.
(Ⅱ) X可取值1,2,3,4,分虽求出相应的概率,由此能求出X的分布列和数学期望.
(Ⅱ) X可取值1,2,3,4,分虽求出相应的概率,由此能求出X的分布列和数学期望.
解答:
解:(Ⅰ)前3次检验的产品中至少1种是乙企业的产品的概率:
P=1-
×
×
=
,
∴前3次检验的产品中至少1种是乙企业的产品的概率为
.…(4分)
(Ⅱ) X可取值1,2,3,4,
P(X=1)=
,
P(X=2)=
×
=
,
P(X=3)=
×
×
=
,
P(X=4)=
×
×
=
,…(9分)
X的分布列如下表:
X的数学期望为:E(X)=1×
+2×
+3×
+4×
=
.…(13分)
P=1-
| 5 |
| 8 |
| 4 |
| 7 |
| 3 |
| 6 |
| 23 |
| 28 |
∴前3次检验的产品中至少1种是乙企业的产品的概率为
| 23 |
| 28 |
(Ⅱ) X可取值1,2,3,4,
P(X=1)=
| 5 |
| 8 |
P(X=2)=
| 3 |
| 8 |
| 5 |
| 7 |
| 15 |
| 56 |
P(X=3)=
| 3 |
| 8 |
| 2 |
| 7 |
| 5 |
| 6 |
| 5 |
| 56 |
P(X=4)=
| 3 |
| 8 |
| 2 |
| 7 |
| 1 |
| 6 |
| 1 |
| 56 |
X的分布列如下表:
| X | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 5 |
| 8 |
| 15 |
| 56 |
| 5 |
| 56 |
| 1 |
| 56 |
| 3 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
相关题目
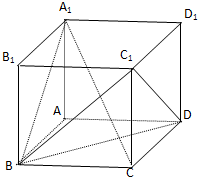 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.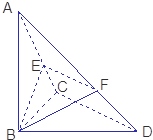 已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且