题目内容
12.在二项式(x-2)5的展开式中,含x3项的系数为( )| A. | -80 | B. | -40 | C. | 40 | D. | 80 |
分析 先求出通项公式,再令x的指数为3,即可求出答案
解答 解:二项式(x-2)5展开式的通项公式为(-2)rC5rx5-r,
令5-r=3,解得r=2,
则二项式(x-2)5的展开式中,含x3项的系数为4C52=40
故选:C
点评 本题考查二项式定理的应用,突出考查二项展开式的通项公式,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.已知cos(θ+$\frac{π}{4}$)•cos(θ-$\frac{π}{4}$)=$\frac{{\sqrt{3}}}{4}$,θ∈($\frac{3π}{4}$,π),则sinθ+cosθ的值为( )
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $-\frac{{\sqrt{6}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
3.若函数f(x)=$\frac{1}{2}$x2-ax+lnx有极值,则a的取值范围是( )
| A. | (-∞,-2) | B. | (-2,2) | C. | (-∞,2)∪(2,+∞) | D. | (2,+∞) |
7.为了调查某班级的作业完成情况,将该班级的52名学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知5号,18号,44号同学在样本中,那么样本中还有一位同学的编号应该是( )
| A. | 23 | B. | 27 | C. | 31 | D. | 33 |
4.已知$a={log_2}3,b={2^{-\frac{1}{3}}},c={log_{\frac{1}{3}}}\frac{1}{30}$,则a、b、c的大小关系是( )
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | c>b>a |
1.把8个相同的小球全部放入编号为1,2,3,4的四个盒中,则不同的放法数为( )
| A. | 35 | B. | 70 | C. | 165 | D. | 1860 |
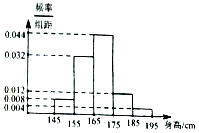 某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.
某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288.