Question

站在河边看对岸的目标A与B，但不能到达．在岸边选取相距1千米的C、D两个观测点，同时测得∠ACB=∠ADC=∠ADB=45°，∠BCD=60°（A、B、C、D在同一平面上），则目标A与B之间的距离为

 

千米．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：利用△ACD的边角关系得出AC，在△BCD中，由勾股定理求出BC，在△ACB中利用余弦定理即可得出AB．

解答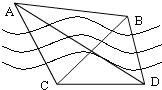： 解：在△ACD中，∠ADC=45°，∠ACD=105°，∴∠CAD=30°．
∴由正弦定理可得

1

sin30°

=

AC

sin45°

，
∴AC=

2

．
在△BDC中，∠CDB=45°+45°=90°，∠BCD=60°
∴BC=2．
由余弦定理，得AB²=AC²+BC²-2AC•BC•cos∠BCA
=2+4-2•

2

•2•

2

2

=2
∴AB=

2

千米．
故答案为：

2

．

点评：本题给出不能到达的两点A、B，利用解三角形的知识求A、B之间的距离．着重考查了特殊三角函数的值、利用正余弦定理解三角形等知识，属于中档题．