题目内容
5．顶点在原点，对称轴是y轴，且顶点与焦点的距离等于6的抛物线标准方程是x2=±24y．分析 利用已知条件，求出抛物线的距离p，然后写出抛物线方程即可．
解答 解：顶点在原点，对称轴是y轴，且顶点与焦点的距离等于6，可得抛物线方程p=12，
所求抛物线方程为：x2=±24y．
故答案为：x2=±24y．
点评 本题考查抛物线的简单性质的应用，考查计算能力．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
16．
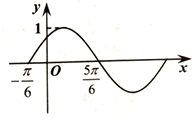函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则关于f（x）的说法正确的是（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则关于f（x）的说法正确的是（ ）| A． | 对称轴方程是x=$\frac{π}{3}$+2kπ（k∈Z） | B． | φ=-$\frac{π}{6}$ | ||
| C． | 最小正周期为π | D． | 在区间（$\frac{π}{2}$，$\frac{7π}{6}$）上单调递减 |
20．已知F1（-3，0），F2（3，0），动点P满足|PF1|-|PF2|=4，则点P的轨迹是（ ）
| A． | 双曲线 | B． | 双曲线的一支 | C． | 一条射线 | D． | 不存在 |
10．已知函数$y=\frac{2}{x}$，当x由2变为1.5时，函数的增量为（ ）
| A． | 1 | B． | 2 | C． | $\frac{1}{3}$ | D． | $\frac{3}{2}$ |
17．如图，在△ABC中，若AB=5，AC=7，∠B=60°，则BC等于（ ）
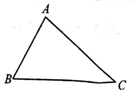
| A． | $5\sqrt{3}$ | B． | $6\sqrt{2}$ | C． | 8 | D． | $5\sqrt{2}$ |