题目内容
16.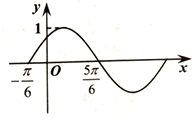 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于f(x)的说法正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则关于f(x)的说法正确的是( )| A. | 对称轴方程是x=$\frac{π}{3}$+2kπ(k∈Z) | B. | φ=-$\frac{π}{6}$ | ||
| C. | 最小正周期为π | D. | 在区间($\frac{π}{2}$,$\frac{7π}{6}$)上单调递减 |
分析 由函数图象可得A,周期T=2[$\frac{5π}{6}$-(-$\frac{π}{6}$)]=2π,可得C错误,利用周期公式可求ω,由点($\frac{5π}{6}$,0)在函数图象上,结合范围|φ|<$\frac{π}{2}$,可得φ=$\frac{π}{6}$,可求B错误,可求函数解析式,令x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,解得函数的对称轴方程可求A错误;令2kπ+$\frac{π}{2}$≤x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得函数的单调递减区间即可判定D正确,从而得解.
解答 解:由函数图象可得:A=1,周期T=2[$\frac{5π}{6}$-(-$\frac{π}{6}$)]=2π,可得C错误,
可得:ω=$\frac{2π}{T}$=$\frac{2π}{2π}$=1,
由点($\frac{5π}{6}$,0)在函数图象上,可得:sin($\frac{5π}{6}$+φ)=0,
解得:φ=kπ-$\frac{5π}{6}$,k∈Z,
又|φ|<$\frac{π}{2}$,可得:φ=$\frac{π}{6}$,故B错误,
可得:f(x)=sin(x+$\frac{π}{6}$).
令x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,解得函数的对称轴方程为:x=kπ+$\frac{π}{3}$,k∈Z,故A错误;
令2kπ+$\frac{π}{2}$≤x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得:2kπ+$\frac{π}{3}$≤x≤2kπ+$\frac{4π}{3}$,k∈Z,
可得函数的单调递减区间为:[2kπ+$\frac{π}{3}$,2kπ+$\frac{4π}{3}$],k∈Z,由于($\frac{π}{2}$,$\frac{7π}{6}$)?[$\frac{π}{3}$,$\frac{4π}{3}$],可得D正确.
故选:D.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了三角函数周期公式,正弦函数的图象和性质的综合应用,考查了数形结合思想和转化思想,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | $\frac{4}{3}$ |
| A. | (0,1] | B. | (-∞,1) | C. | (-∞,1] | D. | (1,+∞) |
| A. | {-1,1} | B. | {-1,0,1} | C. | {1} | D. | {0,1} |
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |