题目内容
20.已知复数z1,z2满足|z1-$\overline{{z}_{2}}$|=|1-z1z2||,则有( )| A. | |z1|<0且|z2|<1 | B. | |z1|<1或|z2|<1 | C. | |z1|=1且|z2|=1 | D. | |z1|=1或|z2|=1 |
分析 利用$|z{|}^{2}=z•\overline{z}$,结合$|{z}_{1}-\overline{{z}_{2}}{|}^{2}=|1-{z}_{1}{z}_{2}{|}^{2}$,化简出$|{z}_{1}{|}^{2}+|{z}_{2}{|}^{2}-1-|\overline{{z}_{1}}{|}^{2}|\overline{{z}_{2}}{|}^{2}=0$,通过分解因式推出z1,z2中至少又一个值为1可得答案.
解答 解:由|z1-$\overline{{z}_{2}}$|=|1-z1z2|,得
$|{z}_{1}-\overline{{z}_{2}}{|}^{2}=|1-{z}_{1}{z}_{2}{|}^{2}$,即$({z}_{1}-\overline{{z}_{2}})(\overline{{z}_{1}-\overline{{z}_{2}}})$=$(1-{z}_{1}{z}_{2})(\overline{1-{z}_{1}{z}_{2}})$,
∴$({z}_{1}-\overline{{z}_{2}})(\overline{{z}_{1}}-{z}_{2})$=$(1-{z}_{1}{z}_{2})(1-\overline{{z}_{1}}\overline{{z}_{2}})$,
∴$|{z}_{1}{|}^{2}-{z}_{1}{z}_{2}-\overline{{z}_{1}}\overline{{z}_{2}}+|{z}_{2}{|}^{2}$=$1-\overline{{z}_{1}}\overline{{z}_{2}}-{z}_{1}{z}_{2}+|\overrightarrow{{z}_{1}}{|}^{2}|\overline{{z}_{2}}{|}^{2}$.
∴$|{z}_{1}{|}^{2}+|{z}_{2}{|}^{2}-1-|\overline{{z}_{1}}{|}^{2}|\overline{{z}_{2}}{|}^{2}=0$,
即$(|{z}_{1}{|}^{2}-1)(|{z}_{2}{|}^{2}-1)=0$.
得$|{z}_{1}{|}^{2}=1$或$|{z}_{2}{|}^{2}=1$.
∴|z1|=1或|z2|=1.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,考查了推理能力与计算能力,属于中档题.

| A. | (0,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
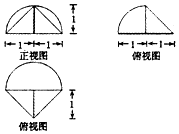
| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π+1}{3}$ | D. | $\frac{2π+1}{3}$ |
f(x)的命题正确的是( )
| A. | f(3)>e2f(1) | B. | f(3)<ef(2) | C. | f(4)<e4f(0) | D. | f(4)<e5f(-1) |
(1)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出计算式即可,不
必计算出结果)
(2)随机抽取8位,他们的数学分数从小到大排序是:60,65,70,75,80,85,90,95,物理分数从
小到大排序是:72,77,80,84,88,90,93,95.
①若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均
为优秀的概率;
②若这8位同学的数学、物理分数事实上对应如表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
参考公式:回归直线的方程是:$\stackrel{∧}{y}$=bx+a,其中对应的回归估计值b=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,
参考数据:$\overline x=77.5$,$\overline y=84.875$,$\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}$≈1050,$\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}$≈688,.