题目内容
16.已知a>0,b>0,且$\frac{1}{a}$+$\frac{2}{b}$=1,则ab的最小值为8.分析 利用基本不等式的性质即可得出.
解答 解:∵a>0,b>0,且$\frac{1}{a}$+$\frac{2}{b}$=1,
∴1≥$2\sqrt{\frac{1}{a}•\frac{2}{b}}$,化为ab≥8,当且仅当a=2,b=4时取等号.
则ab的最小值为8.
故答案为:8.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.复数$\frac{5-i}{i-1}$在复平面上所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.分别在区间[0,$\frac{π}{2}$]和[0,1]内任取两个实数x,y,则不等式y≤cosx恒成立的概率为( )
| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{1}{2}$ |
11.下列命题正确的是( )
| A. | 经过三点确定一个平面 | |
| B. | 经过一条条直线和一个点确定一个平面 | |
| C. | 梯形确定一个平面 | |
| D. | 四边形确定一个平面 |
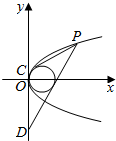 斜率为1的直线l经过抛物线E:y2=2px(p>0)的焦点,且被抛物线所截得弦AB的长为4.
斜率为1的直线l经过抛物线E:y2=2px(p>0)的焦点,且被抛物线所截得弦AB的长为4.