题目内容
1.已知函数f(x)=|x-a|-|x+3|,a∈R.(1)当a=-1时,解不等式f(x)≤1;
(2)不等式f(x)≤4在x∈[-2,3]时恒成立,求a的取值范围.
分析 (1)将a=-1代入f(x),通过讨论x的范围,得到不等式组,解出即可;
(2)问题转化为-7≤a≤2x+7在x∈[-2,3]时恒成立,而2x+7在x∈[-2,3]的最小值是3,从而求出a的范围即可.
解答 解:(1)a=-1时,f(x)=|x+1|-|x+3|≤1,
?$\left\{\begin{array}{l}{x≤-3}\\{-x-1+x+3≤1}\end{array}\right.$或$\left\{\begin{array}{l}{-3<x<-1}\\{-x-1-x-3≤1}\end{array}\right.$或$\left\{\begin{array}{l}{x≥-1}\\{x+1-x-3≤1}\end{array}\right.$,
解得:x≤-1;
(2)∵x∈[-2,3],
∴x+3>0,
∴不等式f(x)≤4在x∈[-2,3]时恒成立,
?|x-a|≤x+7在x∈[-2,3]时恒成立,
?-(x+7)≤x-a≤x+7在x∈[-2,3]时恒成立,
?-x-7-x≤-a≤7在x∈[-2,3]时恒成立,
?-7≤a≤2x+7在x∈[-2,3]时恒成立,
而2x+7在x∈[-2,3]的最小值是3,
∴-7≤a≤3.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
11.已知函数f(x)=x3-12x+8在区间[-3,3]上的最大值与最小值分别为M、m,则$\frac{M}{m}$等于( )
| A. | -24 | B. | -17 | C. | -3 | D. | 3 |
12.过点A(0,2)与抛物线C:y2=4x恰有一个交点的直线有( )条.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
9.下列函数为偶函数的是( )
| A. | f(x)=x | B. | f(x)=x3 | C. | f(x)=x2,x∈(-5,5] | D. | f(x)=4 |
6.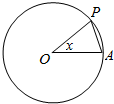 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )
 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )| A. | 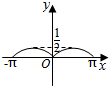 | B. | 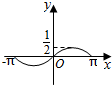 | C. |  | D. | 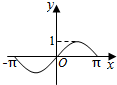 |
13.已知数列{an}满足a4=23,an+1=2an+1,则a2等于( )
| A. | 5 | B. | $\frac{11}{2}$ | C. | 6 | D. | $\frac{13}{2}$ |
10.己知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
| A. | 2 | B. | 3 | C. | $\frac{11}{5}$ | D. | $\frac{37}{16}$ |
11.已知m,n,l为不同的直线,α,β,γ为不同的平面,则下列命题正确的是( )
| A. | 若m?α,n?α,m∥β,n∥β,则α∥β | B. | 若m∥n,n∥α,则m∥α | ||
| C. | 若m⊥α,n⊥α,则m∥n | D. | 若α⊥γ,β⊥γ,则α∥β |