题目内容
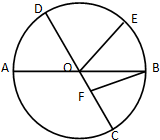 如图所示,在⊙O中,AB与CD是夹角为60°的两条直径,E、F分别是⊙O与直径CD上的动点,若
如图所示,在⊙O中,AB与CD是夹角为60°的两条直径,E、F分别是⊙O与直径CD上的动点,若| OE |
| BF |
| OA |
| OC |
考点:平面向量数量积的运算
专题:函数的性质及应用,三角函数的图像与性质,平面向量及应用
分析:根据题意,建立直角坐标系,用坐标表示B、C、E、F,计算
•
与
•
,求出λ的表达式,求出λ的取值范围即可.
| OE |
| BF |
| OA |
| OC |
解答:
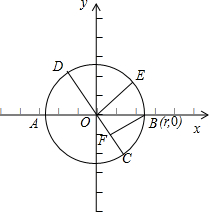 解:设⊙O的半径为r,以O为原点,OB为x轴建立直角坐标系,如图所示;
解:设⊙O的半径为r,以O为原点,OB为x轴建立直角坐标系,如图所示;
则B(r,0),C(
r,-
r),
设E(rcosα,rsinα),α∈(0,π);
∴
=μ
=μ(
r,-
r)=(
μr,-
μr),其中μ∈[-1,1];
∴
=(
μr-r,-
μr),
∴
•
=(rcosα,rsinα)•(
μr-r,-
μr)=r2(
μ-1)cosα-
μr2sinα;
•
=(-r0)•(
r,-
r)=-
r2;
∵
•
+λ
•
=0,
∴λ=-
=(μ-2)cosα-
μsinα=
sin(α+θ)=
sin(α+θ);
又μ∈[-1,1],∴
≤
≤2
,
∴-2
≤
sin(α+θ)≤2
;
∴-2
≤λ≤2
,
即λ的取值范围是[-2
,2
].
故答案为:[-2
,2
].
 解:设⊙O的半径为r,以O为原点,OB为x轴建立直角坐标系,如图所示;
解:设⊙O的半径为r,以O为原点,OB为x轴建立直角坐标系,如图所示;则B(r,0),C(
| 1 |
| 2 |
| ||
| 2 |
设E(rcosα,rsinα),α∈(0,π);
∴
| OF |
| OC |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
| BF |
| 1 |
| 2 |
| ||
| 2 |
∴
| OE |
| BF |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| OA |
| OC |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∵
| OE |
| BF |
| OA |
| OC |
∴λ=-
| ||||
|
| 3 |
| (μ-2)2+3μ2 |
4(μ-
|
又μ∈[-1,1],∴
| 3 |
4(μ-
|
| 3 |
∴-2
| 3 |
| 4(μ-1)2+3 |
| 3 |
∴-2
| 3 |
| 3 |
即λ的取值范围是[-2
| 3 |
| 3 |
故答案为:[-2
| 3 |
| 3 |
点评:本题考查了平面向量的应用问题,也考查了求函数的最值问题以及三角函数的恒等变换问题,是较难的题目.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
当x∈[1,5]时,函数f(x)=3x2-4x+c的值域为( )
| A、[f(1),f(5)] | ||
B、[f(1),f(
| ||
C、[f(
| ||
| D、[c,f(5)] |
函数y=x2+bx+c在区间[0,+∞)上具有单调性,则实数b应满足的条件是( )
| A、b≥0 | B、b≤0 |
| C、b>0 | D、b<0 |
已知向量
=(2cosφ,2sinφ),φ∈(90°,180°),
=(1,1),则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、φ | B、φ-45° |
| C、135°-φ | D、45°-φ |
已知点A(1,5),B(3,9),O为坐标原点,若点C满足
=α
+β
,其中α,β∈R,且α+β=1,则点C的轨迹方程为( )
| OC |
| OA |
| OB |
| A、2x+y-7=0 |
| B、2x-y+3=0 |
| C、x-2y+9=0 |
| D、x+2y-11=0 |
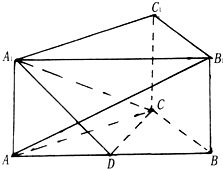 如图所示,在直三棱柱ABC-A1B1C1中,AA1=2,AB=4,AC=BC=3,D为AB的中点,且AB1⊥A1C
如图所示,在直三棱柱ABC-A1B1C1中,AA1=2,AB=4,AC=BC=3,D为AB的中点,且AB1⊥A1C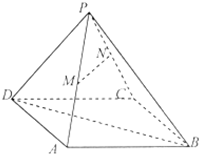 如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2
如图,已知四棱锥P-ABCD,底面四边形ABCD为菱形,AB=2,BD=2