题目内容
18.已知向量$\overrightarrow{a}$=(1,$\sqrt{2}$),$\overrightarrow{b}$=($\frac{1}{2}$,sinθ),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则锐角θ=$\frac{π}{4}$.分析 利用向量平行的坐标关系得到关于θ的方程,求锐角即可.
解答 解:因为$\overrightarrow{a}$∥$\overrightarrow{b}$,所以sin$θ=\frac{\sqrt{2}}{2}$,所以锐角$θ=\frac{π}{4}$;
故答案为:$\frac{π}{4}$.
点评 本题考查了平面向量平行的坐标关系;熟记向量平行的性质是关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
3.函数f(x)=cos(3x+φ)的图象关于原点成中心对称,则φ等于( )
| A. | -$\frac{π}{2}$ | B. | 2kπ-$\frac{π}{2}$(k∈Z) | C. | kπ(k∈Z) | D. | kπ+$\frac{π}{2}$(k∈Z) |
7.已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{17}{18}$ |
8.复数z满足z(1-2i)=3+4i复数z的共轭复数所对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
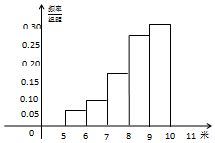 某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.