题目内容
下列结论中正确命题的序号是 (写出所有正确命题的序号).
①积分
cosxdx的值为2;
②若
•
<0,则
与
的夹角为钝角;
③若a、b∈[0,1],则不等式a2+b2<
成立的概率是
;
④函数y=3x+3-x(x>0)的最小值为2.
①积分
| ∫ |
-
|
②若
| a |
| b |
| a |
| b |
③若a、b∈[0,1],则不等式a2+b2<
| 1 |
| 4 |
| π |
| 16 |
④函数y=3x+3-x(x>0)的最小值为2.
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:①求出原函数sinx,再运用积分公式即可;
②利用数量积的定义去判断夹角大小;
③利用几何概型公式求概率;
④使用基本不等式,当条件不成立时,则利用函数的单调性.
②利用数量积的定义去判断夹角大小;
③利用几何概型公式求概率;
④使用基本不等式,当条件不成立时,则利用函数的单调性.
解答:
 解:①积分
解:①积分
cosxdx=sinx
=sin
-sin(-
)
=1-(-1)=2,所以①正确;
②当
与
共线且方向相反时,满足
•
<0,但此时
与
的夹角为180°,所以②错误;
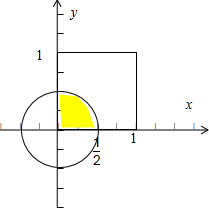
③若a,b∈[0,1],则不等式a2+b2<
成立的概率是p=
=
,如图.所以③正确;
④因为函数y=t+
在t>1时没有最小值,所以函数y=3x+3-x(x>0)没有最小值.所以④错误.
所以正确的有①③.
故答案为:①③.
 解:①积分
解:①积分| ∫ |
-
|
| | |
-
|
| π |
| 2 |
| π |
| 2 |
=1-(-1)=2,所以①正确;
②当
| a |
| b |
| a |
| b |
| a |
| b |
③若a,b∈[0,1],则不等式a2+b2<
| 1 |
| 4 |
| ||||
| 1×1 |
| π |
| 16 |
④因为函数y=t+
| 1 |
| t |
所以正确的有①③.
故答案为:①③.
点评:本题考查各种命题的真假判断,正确利用相关知识进行推理,要求熟练进行应用.

练习册系列答案
相关题目
下列判断正确的是( )
A、函数f(x)=
| ||
| B、函数f(x)=x2-|x|是偶函数 | ||
| C、函数f(x)=x0是非奇非偶函数 | ||
| D、函数f(x)=2既是奇函数又是偶函数 |
设F为抛物线y2=8x的焦点,A,B,C为该抛物线上三点,若
+
+
=
,则|
|+|
|+|
|=( )
| FA |
| FB |
| FC |
| 0 |
| FA |
| FB |
| FC |
| A、6 | B、9 | C、12 | D、16 |
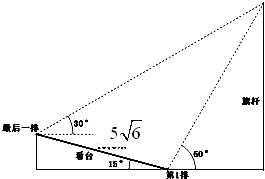 某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5