题目内容
若当-3<x<1时,不等式(1-a)x2-4x+6>0恒成立,则a的取值范围是 .
考点:函数恒成立问题
专题:函数的性质及应用
分析:当x=0时,原不等式即是6>0.成立.当x≠0时,原不等式两边同除以x2,可化为a<
-
+1=
-
+1=6(
-
)2+
,令t=
,则t<-
或t>1,且a<6(t-
)2+
,令f(t)=6(t-
)2+
,根据二次函数性质求其最小值即可.
| 6 |
| x2 |
| 4 |
| x |
| 6 |
| x2 |
| 4 |
| x |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:当x=0时,不等式(1-a)x2-4x+6>0显然成立,
当x≠0时,不等式(1-a)x2-4x+6>0可化为,
a<
+1,
即,a<
-
+1=
-
+1=6(
-
)2+
,
∵-3<x<1且x≠0,
∴
<-
或
>1,
令t=
,则t<-
或t>1,且a<6(t-
)2+
,
令f(t)=6(t-
)2+
,
则根据二次函数性质可知,
f(t)在(-∞,-
)上递减,在(1,+,∞)上递增,且f(-
)=f(1)=3,
∴f(t)>3,
∵当-3<x<1时,不等式(1-a)x2-4x+6>0恒成立,
∴a≤3.
故答案为:(-∞,3].
当x≠0时,不等式(1-a)x2-4x+6>0可化为,
a<
| 6-4x |
| x2 |
即,a<
| 6 |
| x2 |
| 4 |
| x |
| 6 |
| x2 |
| 4 |
| x |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
∵-3<x<1且x≠0,
∴
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| x |
令t=
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
令f(t)=6(t-
| 1 |
| 3 |
| 1 |
| 3 |
则根据二次函数性质可知,
f(t)在(-∞,-
| 1 |
| 3 |
| 1 |
| 3 |
∴f(t)>3,
∵当-3<x<1时,不等式(1-a)x2-4x+6>0恒成立,
∴a≤3.
故答案为:(-∞,3].
点评:本题考查二次函数与一元二次不等式的关系,以及转化与化归的思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知实数x,y满足
,则z=x+y的最大值是( )
|
| A、0 | B、2 | C、4 | D、8 |
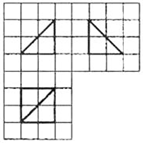 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的体积为
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的体积为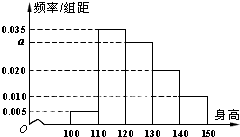 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a=