题目内容
设函数f（x）=
+1，若a，b，c成等差数列（公差不为零），则f（a）+f（c）= ．
| 1 |
| x-b |
考点：等差数列的性质,函数的值
专题：等差数列与等比数列
分析：由题意可得2b=a+c，化简可得f（a）+f（c）=2+
，代入化简可得．
| c+a-2b |
| (a-b)(c-b) |
解答：
解：∵a，b，c成等差数列，∴2b=a+c，
∴f（a）+f（c）=
+1+
+1
=2+
+
=2+
=2+
=2+0=2
故答案为：2
∴f（a）+f（c）=
| 1 |
| a-b |
| 1 |
| c-b |
=2+
| 1 |
| a-b |
| 1 |
| c-b |
| c-b+a-b |
| (a-b)(c-b) |
=2+
| c+a-2b |
| (a-b)(c-b) |
故答案为：2
点评：本题考查等差数列的性质，涉及分式的加减运算，属基础题．
练习册系列答案
相关题目
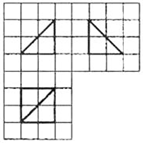如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体外接球的体积为