题目内容
已知实数a、b、c满足条件0≤a+c-2b≤1,且2a+2b≤21+c,则
的取值范围是 .
| 2a-2b |
| 2c |
考点:简单线性规划
专题:数形结合,转化思想
分析:由2a+2b≤21+c,得2a-c+2b-c≤2,由0≤a+c-2b≤1得0≤(a-c)-2(b-c)≤1,然后由指数函数的单调性得到1≤2(a-c)-2(b-c)≤2,再令x=2b-c,y=2a-c,即可得到x+y≤2,x2≤y≤2x2,x>0,y>0,则求
的范围可转化为求目标函数t=y-x的范围.然后利用线性规划知识求解.
| 2a-2b |
| 2c |
解答:
解:由2a+2b≤21+c,得2a-c+2b-c≤2,
由0≤a+c-2b≤1,得0≤(a-c)-2(b-c)≤1,
于是有1≤2(a-c)-2(b-c)≤2,
即1≤
≤2.设x=2b-c,y=2a-c,
则有x+y≤2,x2≤y≤2x2,x>0,y>0,
=y-x.
在平面直角坐标系xOy中作出点(x,y)所表示的平面区域,并设y-x=t.
如图,
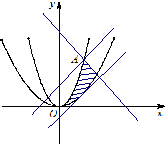
当直线y-x=t与曲线y=x2相切时,t最小.
此时令y′=2x=1,解得x=
,于是y=
,
∴tmin=
-
=-
.
当直线过点A时,t最大.
由
,解得A(
,
),
∴tmax=
-
=
.
因此
的取值范围是[-
,
].
故答案为:[-
,
].
由0≤a+c-2b≤1,得0≤(a-c)-2(b-c)≤1,
于是有1≤2(a-c)-2(b-c)≤2,
即1≤
| 2a-c |
| 22(b-c) |
则有x+y≤2,x2≤y≤2x2,x>0,y>0,
| 2a-2b |
| 2c |
在平面直角坐标系xOy中作出点(x,y)所表示的平面区域,并设y-x=t.
如图,

当直线y-x=t与曲线y=x2相切时,t最小.
此时令y′=2x=1,解得x=
| 1 |
| 2 |
| 1 |
| 4 |
∴tmin=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
当直线过点A时,t最大.
由
|
-1+
| ||
| 4 |
9-
| ||
| 4 |
∴tmax=
9-
| ||
| 4 |
-1+
| ||
| 4 |
5-
| ||
| 2 |
因此
| 2a-2b |
| 2c |
| 1 |
| 4 |
5-
| ||
| 2 |
故答案为:[-
| 1 |
| 4 |
5-
| ||
| 2 |
点评:本题含三个变量,解题时要注意通过换元减少变量的个数.利用消元、换元等方法进行减元的思想是近年高考填空题中难点和热点,对于层次很好的学生值得关注.该题属难题.

练习册系列答案
相关题目
在边长为3的等边三角形ABC中,点D、E分别在AB、AC上,且满足
=2
,
=
,则
•
=( )
| AD |
| DB |
| AE |
| 1 |
| 2 |
| EC |
| BE |
| CD |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列命题中真命题是( )
| A、“a>b”是“a2>b2”的充分条件 |
| B、“a>b”是“a2>b2”的必要条件 |
| C、“a>b”是“ac2>bc2”的必要条件 |
| D、“a>b”是“|a|>|b|”的充分条件 |
在等比数列{an}中,a3+a5=6,a4=2
,则a2+a6=( )
| 2 |
A、5
| ||
B、4
| ||
| C、8 | ||
| D、4 |

