题目内容
下列命题中真命题是( )
| A、“a>b”是“a2>b2”的充分条件 |
| B、“a>b”是“a2>b2”的必要条件 |
| C、“a>b”是“ac2>bc2”的必要条件 |
| D、“a>b”是“|a|>|b|”的充分条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质,结合充分条件和必要条件的定义即可的结论.
解答:
解:A.当a=1,b=-1,满足a>b,但a2>b2,不成立,即充分性不成立,
B.当a=-1,b=0,满足a2>b2,但a>b不成立,即必要性不成立.
C.当c=0时,ac2>bc2,不成立,即充分性不成立,若ac2>bc2,则必有c≠0,则a>b成立,即“a>b”是“ac2>bc2”的必要条件,成立,
D.当a=1,b=-1,满足a>b,但“|a|>|b|”不成立,即充分性不成立,
故选:C
B.当a=-1,b=0,满足a2>b2,但a>b不成立,即必要性不成立.
C.当c=0时,ac2>bc2,不成立,即充分性不成立,若ac2>bc2,则必有c≠0,则a>b成立,即“a>b”是“ac2>bc2”的必要条件,成立,
D.当a=1,b=-1,满足a>b,但“|a|>|b|”不成立,即充分性不成立,
故选:C
点评:本题主要考查充分条件和必要条件的判定,利用不等式的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线C:x2=8y与直线y=2x-2相交于A,B两点,点P是抛物线C上不同A,B的一点,若直线PA,PB分别与直线y=2相交于点Q,R,O为坐标原点,则
•
的值是( )
| OR |
| OQ |
| A、20 | B、16 |
| C、12 | D、与点P位置有关的一个实数 |
若数列{an}满足:a1=1,a2=2,anan-2=an-1(n≥3),则a2012的值为( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、22012 |
以椭圆
+
=1(a>b>0)的长轴A1A2为一边向外作一等边三角形A1A2P,若随圆的一个短轴的端点B恰为三角形A1A2P的重心,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知F是抛物线y2=4x的焦点,准线与x轴的交点为M,点N在抛物线上,且|NF|=
|MN|,则∠FMN=( )
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、75° |
函数f(x)=lg(x+1)+lg(x-1)的奇偶性是( )
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、既奇又偶函数 |
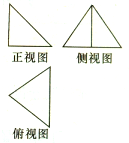 某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )
某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
| D、a3 |