题目内容
4．如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该多面体的表面积为（ ）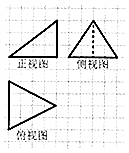
| A． | 20+3$\sqrt{2}$ | B． | 16+8$\sqrt{2}$ | C． | 18+3$\sqrt{5}$ | D． | 18+6$\sqrt{5}$ |
分析 几何体是以俯视图为底面，有一侧棱垂直于底面的三棱锥，由图中数据求出该多面体的表面积．
解答 解：几何体是以俯视图为底面，有一侧棱垂直于底面的三棱锥，
该多面体的表面积为$\frac{1}{2}×4×4$+$\frac{1}{2}×4×5$+$\frac{1}{2}×3×\sqrt{4+16}$×2=18+6$\sqrt{5}$，
故选D．
点评 本题考查由三视图由面积，考查学生的计算能力，确定直观图的形状是关键．
练习册系列答案
相关题目
19．命题“对任意的x∈R，x2-x+1≥0”的否定是（ ）
| A． | 不存在x0∈R，x02-2x0+1≥0 | B． | 存在x0∈R，x02-2x0+1≤0 | ||
| C． | 存在x0∈R，x02-2x0+1＜0 | D． | 对任意的x∈R，x2-2x+1＜0 |
16．若定义在R上的函数f（x）当且仅当存在有限个非零自变量x，使得f（-x）=f（x），则称f（x）为类偶函数，则下列函数中为类偶函数的是（ ）
| A． | f（x）=cosx | B． | f（x）=sinx | C． | f（x）=x2-2x | D． | f（x）=x3-2x |