题目内容
19.命题“对任意的x∈R,x2-x+1≥0”的否定是( )| A. | 不存在x0∈R,x02-2x0+1≥0 | B. | 存在x0∈R,x02-2x0+1≤0 | ||
| C. | 存在x0∈R,x02-2x0+1<0 | D. | 对任意的x∈R,x2-2x+1<0 |
分析 根据含量词的命题的否定形式:将“任意”换为“存在”,同时将结论否定,得到命题的否定.
解答 解:命题“对任意的X∈R,x2-x+1≥0”的否定是
“存在x0∈R,x02-2x0+1<0”
故选:C
点评 求含量词的命题的否定:一般先将量词“任意”与“存在”交换,同时将结论否定即可.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
4.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积为( )
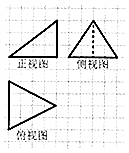

| A. | 20+3$\sqrt{2}$ | B. | 16+8$\sqrt{2}$ | C. | 18+3$\sqrt{5}$ | D. | 18+6$\sqrt{5}$ |
9.定义在R上的函数f(x)的图象关于y轴对称,且f(x)在[0,+∞)上单调递减,若关于x的不等式f(2mx-lnx-3)≥2f(3)-f(-2mx+lnx+3)在x∈[1,3]上恒成立,则实数m的取值范围为( )
| A. | [$\frac{1}{2e}$,$\frac{ln6+6}{6}$] | B. | [$\frac{1}{e}$,$\frac{ln6+6}{3}$] | C. | [$\frac{1}{e}$,$\frac{ln3+6}{3}$] | D. | [$\frac{1}{2e}$,$\frac{ln3+6}{6}$] |