题目内容
 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.
(1)求证:CE∥平面A1BD
(2)若H为A1B上的动点,CH与平面A1AB所成的最大角的正切值为
| ||
| 2 |
(3)在(2)的条件下,求二面角I-BD-A的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明四边形GDCE是平行四边形,利用平行四边形的性质可以证明;
(2)先说明连接EH,则∠EHC为CH与平面AA1B所成的角,再在△CEH中,利用正切函数,即可得到结论;
(3)利用面积比,即可求出二面角I-BD-A的余弦值.
(2)先说明连接EH,则∠EHC为CH与平面AA1B所成的角,再在△CEH中,利用正切函数,即可得到结论;
(3)利用面积比,即可求出二面角I-BD-A的余弦值.
解答:
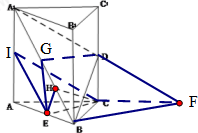 解:(1)取BA1的中点G,连接EG,DG,
解:(1)取BA1的中点G,连接EG,DG,
∴GE平行且等于
AA1,
∵D是CC1中点,
∴CD平行且等于
AA1,
∴GE平行且等于CD,
∴四边形GDCE是平行四边形,
∴CE∥GD,
∵CE?平面A1BD,GD?平面A1BD,
∴CE∥平面A1BD,
(2)∵AA1⊥面ABC,CE?面ABC,
∴AA1⊥CE,
又△ABC等边三角形,E是中点,
∴CE⊥AB,CE=
AB=
,
所以CE⊥面AA1B,
连接EH,则∠EHC为CH与平面AA1B所成的角,
在Rt△CEH中,tan∠EHC=
=
,
所以EH最短时∠EHC最大,
此时,EH⊥A1B,∴tan∠EHC=
=
=
,
∴EH=
由平几相似关系得AA1=4;
(3)△IBD中,IB=DB=2
,ID=4,∴S△IBD=
×2×2=2,
△ABD中,AB=4,DB=2
,AD=2
,∴cos∠ABD=
=
,
∴sin∠ABD=
,
∴S△ABD=
×4×2
×
=
,
∴二面角I-BD-A的余弦值为
=
.
 解:(1)取BA1的中点G,连接EG,DG,
解:(1)取BA1的中点G,连接EG,DG,∴GE平行且等于
| 1 |
| 2 |
∵D是CC1中点,
∴CD平行且等于
| 1 |
| 2 |
∴GE平行且等于CD,
∴四边形GDCE是平行四边形,
∴CE∥GD,
∵CE?平面A1BD,GD?平面A1BD,
∴CE∥平面A1BD,
(2)∵AA1⊥面ABC,CE?面ABC,
∴AA1⊥CE,
又△ABC等边三角形,E是中点,
∴CE⊥AB,CE=
| ||
| 2 |
| 3 |
所以CE⊥面AA1B,
连接EH,则∠EHC为CH与平面AA1B所成的角,
在Rt△CEH中,tan∠EHC=
| CE |
| EH |
| ||
| EH |
所以EH最短时∠EHC最大,
此时,EH⊥A1B,∴tan∠EHC=
| CE |
| EH |
| ||
| EH |
| ||
| 2 |
∴EH=
2
| ||
| 5 |
由平几相似关系得AA1=4;
(3)△IBD中,IB=DB=2
| 2 |
| 1 |
| 2 |
△ABD中,AB=4,DB=2
| 2 |
| 5 |
| 16+8-20 | ||
2×4×2
|
| ||
| 8 |
∴sin∠ABD=
| ||
| 8 |
∴S△ABD=
| 1 |
| 2 |
| 2 |
| ||
| 8 |
| 31 |
∴二面角I-BD-A的余弦值为
| 2 | ||
|
2
| ||
| 31 |
点评:本题考查线面垂直,线面平行,考查线面角,面面角,解题的关键是掌握面面平行的判定方法,正确作出线面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
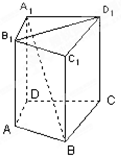 如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件
如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件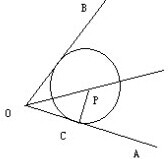 如图,点P是∠AOB平分线上一点,PC⊥OA,垂足为C,OB与以P为圆心、PC为半径的圆相切吗?为什么?
如图,点P是∠AOB平分线上一点,PC⊥OA,垂足为C,OB与以P为圆心、PC为半径的圆相切吗?为什么?