题目内容
16. 如图,四边形ABCD是正方形,四边形ABEG是平行四边形,且平面ABCD⊥平面ABEG,AE⊥AB,EF⊥AG于F,设线段CD、AE的中点分别为P、M.
如图,四边形ABCD是正方形,四边形ABEG是平行四边形,且平面ABCD⊥平面ABEG,AE⊥AB,EF⊥AG于F,设线段CD、AE的中点分别为P、M.(Ⅰ)求证:EF⊥平面BCE;
(Ⅱ)求证:MP∥平面BCE;
(Ⅲ)若∠EAF=30°,求三棱锥M-BDP和三棱锥F-BCE的体积之比.
分析 (Ⅰ)由已知结合面面垂直的性质可得BC⊥平面ABEG,得到EF⊥BC.再由已知证得EF⊥BE,利用线面垂直的判定可得EF⊥平面BCE;
(Ⅱ)设线段AB的中点为N,连接MN,PN.由三角形中位线定理可得MN∥BE,PN∥BC,再由面面平行的判定得平面MNP∥平面BCE,得MP∥平面BCE;
(Ⅲ)设正方形ABCD的边长为a,连接MB,MD,BD,BP,解三角形可得VM-BDP,同理可得VF-BCE,则三棱锥M-BDP和三棱锥F-BCE的体积之比可求.
解答 (Ⅰ)证明:∵平面ABCD⊥平面ABEG,平面ABCD∩平面ABEG=AB,
由ABCD为正方形,得BC⊥AB,
∴BC⊥平面ABEG,又EF?平面ABEG,
∴EF⊥BC.
又四边形ABEG为平行四边形,EF⊥AG,∴EF⊥BE,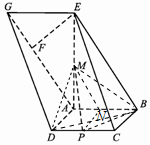
又BE?平面BCE,BC?平面BCE,BC∩BE=B,
∴EF⊥平面BCE;
(Ⅱ)证明:设线段AB的中点为N,连接MN,PN.
∵线段CD、AE的中点分别为P、M,
∴MN∥BE,PN∥BC,则平面MNP∥平面BCE,
故MP∥平面BCE;
(Ⅲ)解:设正方形ABCD的边长为a,连接MB,MD,BD,BP,
∵∠EAF=30°,则EF=$\frac{1}{2}AE$,∠AEB=30°,
∴BE=2AB=2a,
∴${V}_{M-BDP}=\frac{1}{3}{S}_{△BDP}•AM=\frac{1}{3}•\frac{1}{4}{a}^{2}•\frac{1}{2}AE$=$\frac{1}{24}{a}^{2}•AE$.
同理,连接FB,FC,则${V}_{F-BCE}=\frac{1}{3}{S}_{EBC}•EF$=$\frac{1}{3}•\frac{1}{2}•a•2a•\frac{1}{2}AE=\frac{1}{6}{a}^{2}•AE$.
∴VM-BDP:VF-BCE=1:4.
点评 本题考查直线与平面平行、直线与平面垂直的判定,考查空间想象能力和思维能力,训练了多面体体积的求法,是中档题.

| A. | 0 | B. | 10 | C. | 12 | D. | 24 |
| A. | (-1,4] | B. | (2,4] | C. | (3,4) | D. | {3,4} |
 如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )
如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向左平行移动$\frac{1}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{2}{3}$个单位长度 | D. | 向左平行移动$\frac{2π}{3}$个单位长度 |
| A. | ab<ac | B. | ba>ca | C. | logab<logac | D. | $\frac{a}{b}>\frac{a}{c}$ |
| A. | 2$\sqrt{2}$ | B. | $\sqrt{17}$ | C. | $\sqrt{15}$ | D. | 2$\sqrt{5}$ |
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{17}$ |