题目内容
6.已知sin($\frac{3π}{2}$-θ)+3cos(π-θ)=sin(-θ),则sinθcosθ+cos2θ=( )| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{17}$ |
分析 根据三角函数的诱导公式结合同角的三角函数关系式以及弦化切进行化简即可.
解答 解:由sin($\frac{3π}{2}$-θ)+3cos(π-θ)=sin(-θ),
得cosθ-3cosθ=-sinθ,
即-2cosθ=-sinθ,得sinθ=2cosθ,即tanθ=2,
则sinθcosθ+cos2θ═$\frac{sinθcosθ+cos^2θ}{sin^2θ+cos^2θ}$=$\frac{tanθ+1}{tan^2θ+1}$=$\frac{2+1}{4+1}$=$\frac{3}{5}$,
故选:C.
点评 本题主要考查三角函数值的计算,根据三角函数的诱导公式以及同角的三角函数关系式,以及1的代换是解决本题的关键.

练习册系列答案
相关题目
17.已知$sinα=\frac{3}{5}$,且角α的终边在第二象限,则tanα=( )
| A. | 30° | B. | $-\frac{3}{4}$ | C. | $\frac{{10\sqrt{3}}}{3}$ | D. | $5\sqrt{2}$ |
11.实数x,y满足不等式组:$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,若z=x2+y2,则z的取值范围是[0,4].
18.定义$\frac{n}{{P}_{1}+{P}_{2}+…+{P}_{n}}$为n个正数P1,P2…Pn的“均倒数”,若已知正整数数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}+1}{4}$,则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{10}{b}_{11}}$=( )
| A. | $\frac{1}{11}$ | B. | $\frac{1}{12}$ | C. | $\frac{10}{11}$ | D. | $\frac{11}{12}$ |
15.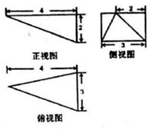 某几何体的三视图如图所示,则该几何体中最长的棱长为( )
某几何体的三视图如图所示,则该几何体中最长的棱长为( )
 某几何体的三视图如图所示,则该几何体中最长的棱长为( )
某几何体的三视图如图所示,则该几何体中最长的棱长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{21}$ | D. | 2$\sqrt{5}$ |
16.点P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$右支上的一点,其左、右焦点分别为F1,F2,若△PF1F2的内切圆I与x轴相切于点A,过F2作PI的垂线,重足为B,O为坐标原点,那么$\frac{{|{OA}|}}{{|{OB}|}}$的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{b}{a}$ | D. | $\frac{a}{b}$ |
 如图,四边形ABCD是正方形,四边形ABEG是平行四边形,且平面ABCD⊥平面ABEG,AE⊥AB,EF⊥AG于F,设线段CD、AE的中点分别为P、M.
如图,四边形ABCD是正方形,四边形ABEG是平行四边形,且平面ABCD⊥平面ABEG,AE⊥AB,EF⊥AG于F,设线段CD、AE的中点分别为P、M.